DSCI 554 lecture 9

Statistics review, statistical graphics

Dr. Luciano Nocera

Outline

Basics of statistics and modeling
Statistical graphics
Tools

Statistics

Types of statistics

Descriptive statistics: summarize the data, i.e. one number stands for a group of numbers
Examples: mean, median, SD
Inferential statistics: infer (model) population data from sample data
Examples: hypothesis testing, regression analysis

Nomenclature

Observed	ML	Stats
Observations	Samples	Cases
Attribute	Feature	Independent variable
Class	Label	Dependent variable

$$\text{dependent variable} = f(\text{independent variables})$$ $$\text{label} = f(\text{features})$$

What are the independent and dependent variables?

Height depends on age


						Time spent studying affects test score


						Medication in persons with Parkinson's Disease affects the SD of the step length

Measures of order

K^th order statistic: value at position k in ordered data

Range: range of values

Modes/peaks: most frequent values

$$ \text{data} = [X_{1},\dots,X_{N}] = [0, 1, 1, 2, 2, 3, 4, 15] \\ 1^{st} \text{order: } X_{1} = \min(X_{1},\dots,X_{N}) = 0 \\ N^{st} \text{order: } X_{N} = \max(X_{1},\dots,X_{N}) = 15 \\ \text{range: } X_{N} - X_{1} = 15 \\ \text{modes: } \{1, 2\} $$

Quantiles

Quantiles are robust to outliers.
q-quantiles ($q-1$ values) divide the observations in $q$ groups.
Ex: 4-quintiles or quartiles ($Q_1, Q_2, Q_3$) divide the data in 4
- $Q_1$ s.t. $25\%$ at or below and $75\%$ above
- $Q_2$ s.t. $50\%$ at or below and $50\%$ above (median)
- $Q_3$ s.t. $75\%$ at or below and $25\%$ above

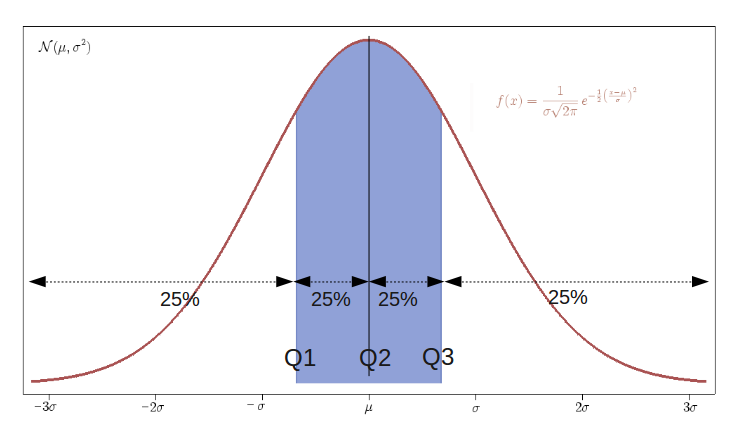
Quartiles in a normal distribution [Ark0n derivative work: Gato ocioso]

$$\text{data} = [0, 1, 1, 2, 2, 3, 4, 15] \\ Q_1 = 1, Q_2 = 2, Q_3 = 3.25$$ Based on SciPy formulation. In the example $N=8$ with N+1 parts. k-th q-quantile: $p = k/q$, $h = (N + 1)p$, $x{\lfloor}h{\rfloor} + (h − {\lfloor}h{\rfloor}) (x{\lfloor}h{\rfloor} + 1 − x{\lfloor}h{\rfloor})$

Measures of central tendency

Median: value in the middle

Mean: sum divided by N $$ \mu = \bar{X} = \sum_{i = 1}^{N}{\frac{X_i}{N}} $$ Standard deviation: dispersion $$\sigma = \sqrt{ \frac{1}{N - 1} \sum_{i}^{N}{({X_i - \bar{X}})^{2}}}$$ Variance: variation around the mean $$\sigma^2$$

Median and mean (adapted from Cmglee - Own work)

Normal distribution where each band has a width of 1 $\sigma$ (M. W. Toews - Own work)

$$ \text{data} = [0, 1, 1, 2, 2, 3, 4, 15] \\ \text{median: } \tilde{X} = 2 \\ \text{mean: } \bar{X} = 3.5 \\ \text{standard deviation: } \sigma = 4.810702 \\ \text{variance: } \sigma^2 = 23.142857 $$

Skewness

negative skew
left-skewed
left-tailed
skewed to the left

0 skewness
symmetric unimodal (not implied)

positive skew
right-skewed
right-tailed
skewed to the right

Frequency & Relative frequency

Frequency: times event $i$ occurs $$n_i$$

Relative frequency: frequency normalized $$f_i = \frac{n_i}{N}$$ with $$N = \sum_{k=1}^{K} n_{k}$$

$$ \text{data} = [A, B, B, A, C, A, C, A] \\ \text{ } \\ n_A = 4, n_B = 2, n_c = 2 \\ \text{ } \\ f_A = \frac{4}{8} = 0.5, f_B = \frac{2}{8} = 0.25, f_C = \frac{2}{8} = 0.25 \\ \text{ } \\ N = n_A + n_B + n_c = 4 + 2 + 2 = 8 $$

Data types

Statistic	Nominal	Ordinal	Interval	Ratio
Frequency	Yes	Yes	Yes	Yes
Median and percentile	No	Yes	Yes	Yes
Mean, SD, SEM^*	No	No	Yes	Yes
Ratio, rate of variation	No	No	No	Yes

* standard error of the mean (SEM): $\sigma_{\bar{X}} = \frac{\sigma}{\sqrt{N}}$

Outline

Basics of statistics and modeling
Statistical graphics
Tools

Importance of graphing before analysis [Anscombe73]

Anscombe's quartet

library(ggplot2)
					library(gridExtra)
					grid.arrange(
						ggplot(anscombe) + geom_point(aes(x1, y1)) +
						geom_abline(intercept = 3, slope = 0.5, color = "red"),
						ggplot(anscombe) + geom_point(aes(x2, y2)) +
						geom_abline(intercept = 3, slope = 0.5, color = "red"),
						ggplot(anscombe) + geom_point(aes(x3, y3)) +
						geom_abline(intercept = 3, slope = 0.5, color = "red"),
						ggplot(anscombe) + geom_point(aes(x4, y4)) +
						geom_abline(intercept = 3, slope = 0.5, color = "red"))

Scatterplot

Shows distribution modes, skewness, outliers

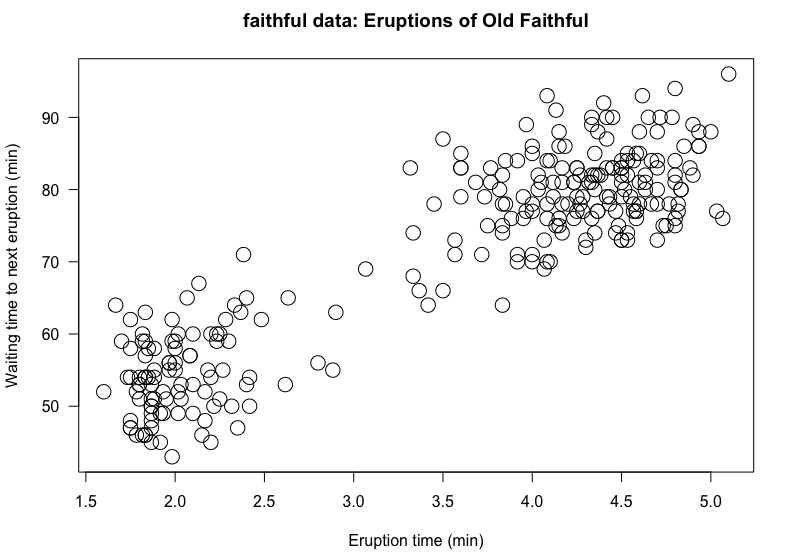
Waiting time between eruptions and the duration of the eruption for the Old Faithful Geyser in Yellowstone National Park, Wyoming, USA. The chart suggests there are two "types" of eruptions: short-wait-short-duration, and long-wait-long-duration.

Scatterplot matrix

Shows distribution for multivariate data

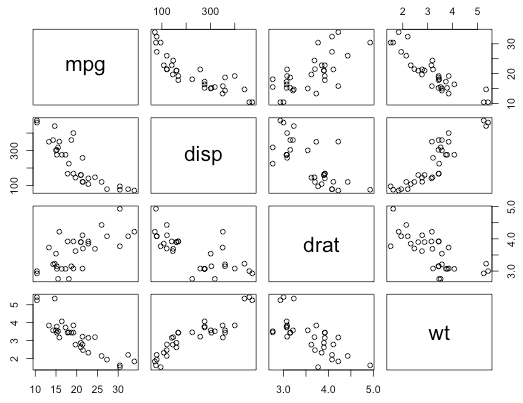
Stripchart (1D scatterplot)

Good for comparison across categories

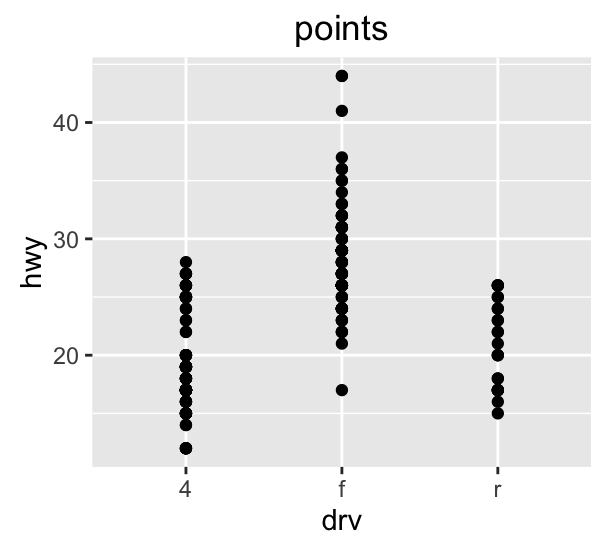
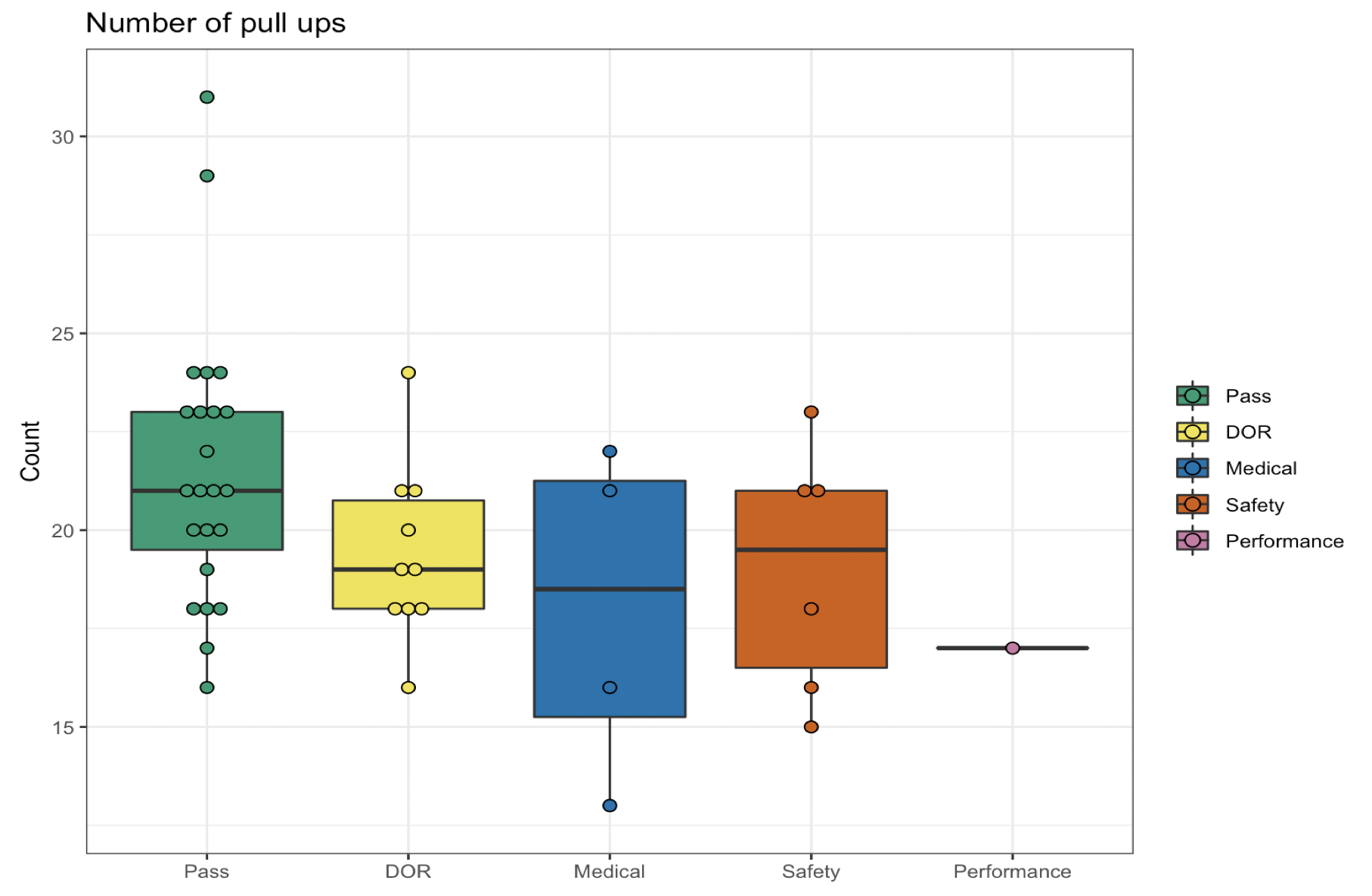
Boxplot or box-and-whisker plot [Tuckey 1969]

Quartiles, distribution skewness, tails, outliers (not modes: unimodal distribution)

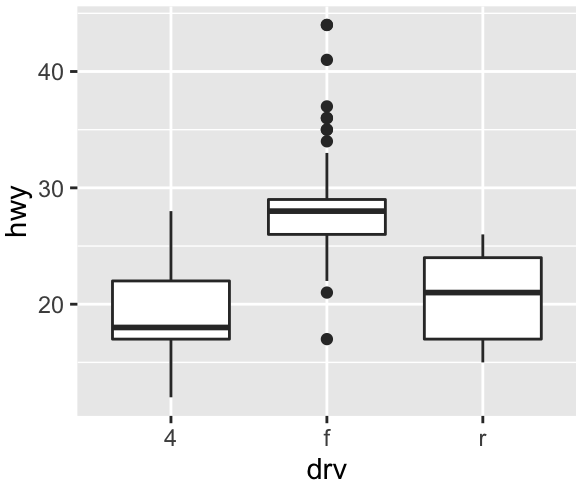
Boxplot anatomy

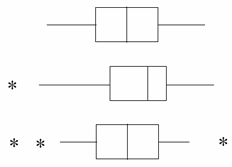
normal distribution

left skewed

centered with outliers

Minimalistic boxplots

Boxplot with notches

Violin plot: mirrored probability density (works for multimodal distributions!)

Boxplot with dotplot

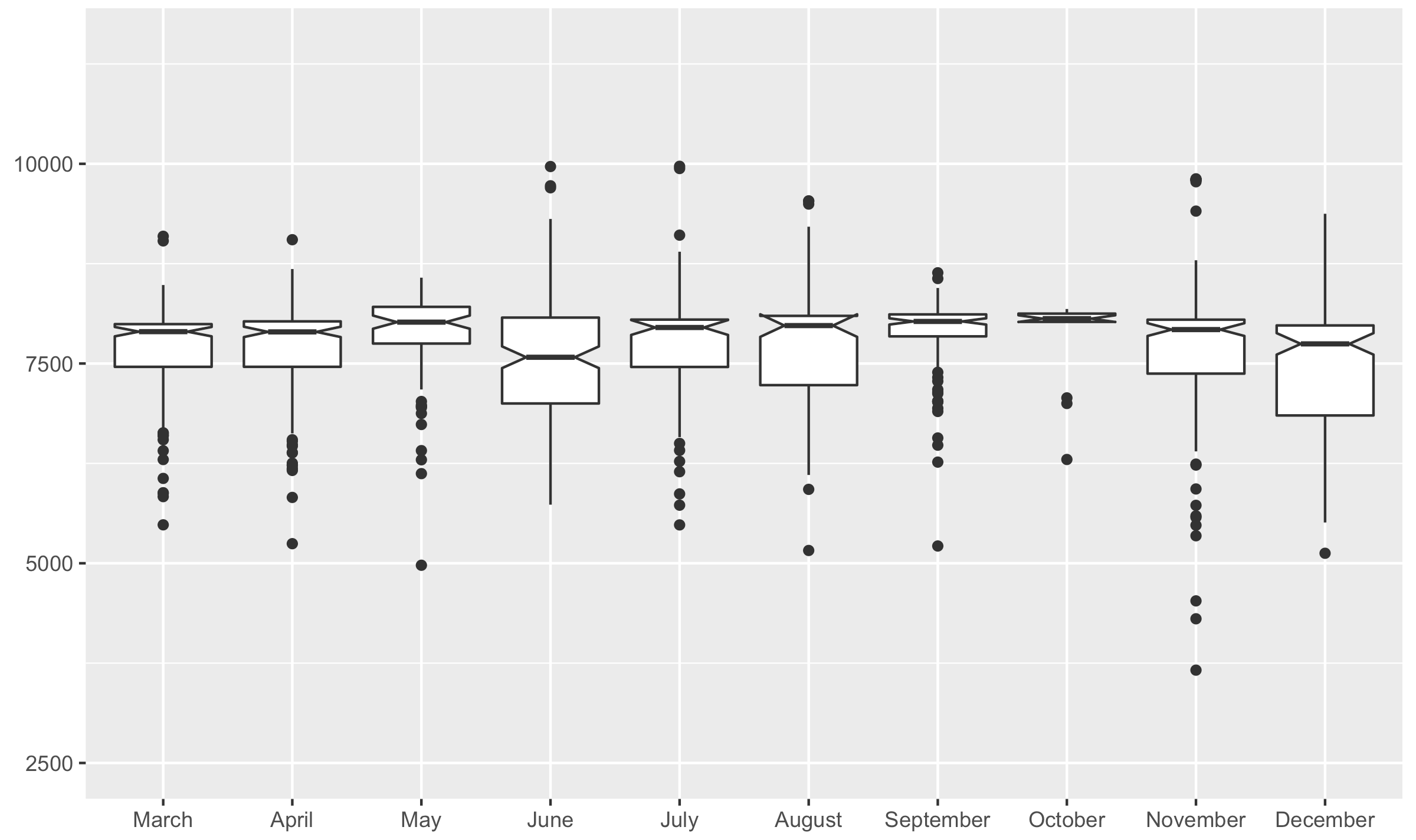
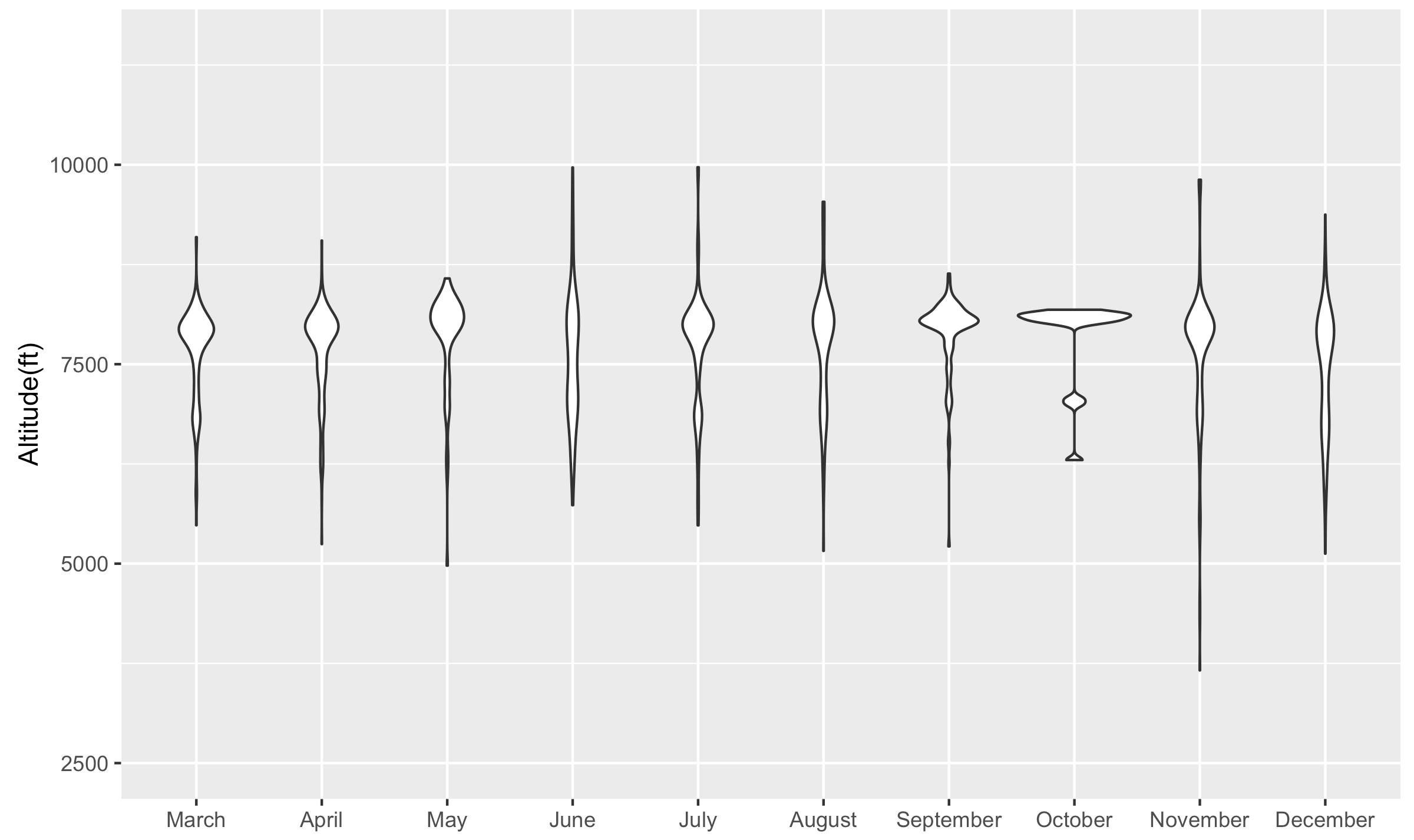
Frequency distribution table

Often shown with ordered data, relative frequency and cumulative frequency

Chol. (mg/dl)	No.	Rel. Freq.	Cum. Freq.
80-119	13	1.2	1.2
120-159	150	14.1	15.3
160-199	442	41.4	56.7
200-239	299	28.0	84.7
240-279	115	10.8	95.5
280-319	34	3.2	98.7
320-359	9	0.8	99.5
360-399	5	0.5	100.0

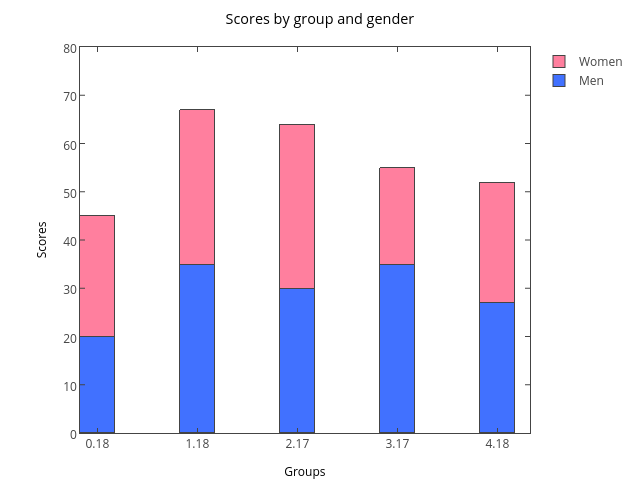
Frequencies of serum cholesterol levels for 1,067 US males, 25-34 years,1976-80

Bar charts of frequencies

Bars separation used to imply discontinuity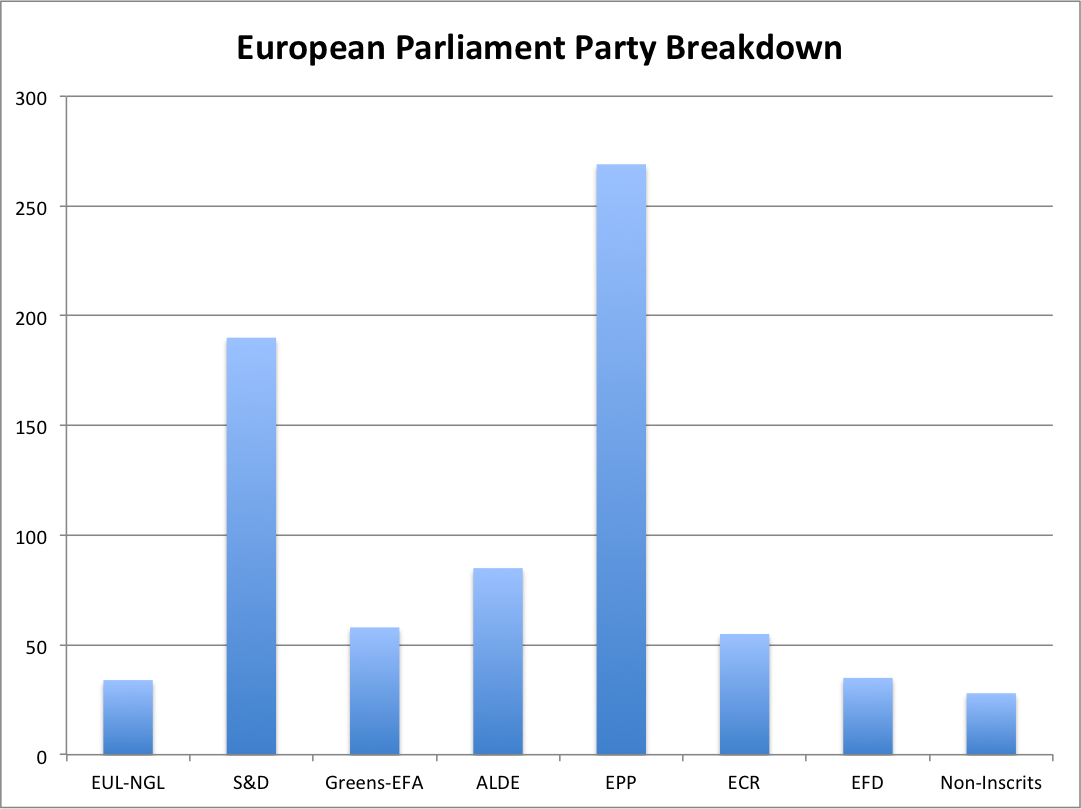

Bars for groups

Stacked bars for subgroups

Population pyramid shows the distribution of age groups within a population Stacked with shift of origin

Stem-and-leaf plot

Shows the data and data distribution (skewness, modes, tails, outliers)

Figure 2. Distribution of cerebellar weights in the F2 intercross as illustrated by stem-and-leaf plots. The values on the left are the observed values, those on the right reflect correction by regression for brain weight. The mean for both distributions is marked by a horizontal line. Airey DC, Lu L, Williams RW Genetic control of the mouse cerebellum: identification of quantitative trait loci modulating size and architecture. J Neuroscience, 2001.

Steps to build a stem-and-leaf plot


					73, 42, 67, 78, 99, 84, 91, 82, 86, 122

Order in ascending order


						42, 67, 73, 78, 82, 84, 86, 91, 99, 122

Select stem and leaf


							42, 67, 73, 78, 82, 84, 86, 91, 99, 122

Plot

Half the size

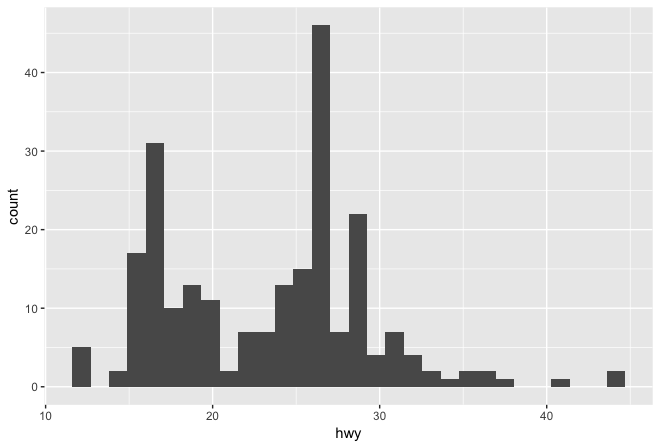
Histogram [Pearson 1895]

Shows skewness, modes, tails, outliers

Bar graph of frequencies for ordered, equal size bins
Bars touch to imply continuity of bins
Need to experiment with the bin size

File:Black cherry tree histogram.svg from Wikimedia Commons

Steps to build an histogram


				73, 42, 67, 78, 99, 84, 91, 82, 86, 122

Order in ascending order


						42, 67, 73, 78, 82, 84, 86, 91, 99, 122

Select bin size

 range = max - min = 122 - 42 = 80
 bin size 20
 bin size 40

Create a frequency table

Interval	Frequency
40-60	1
60-80	3
80-100	5
100-120	0
120-140	1

Bin size 20

Interval	Frequency
40-80	4
80-120	5
120-140	1

Bin size 40

Plot

Frequency polygon

Shows skewness, modes, tails, outliers

Histogram

Frequency polygon

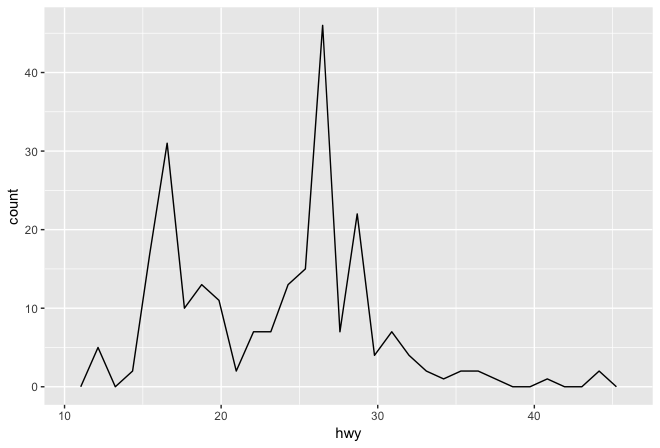
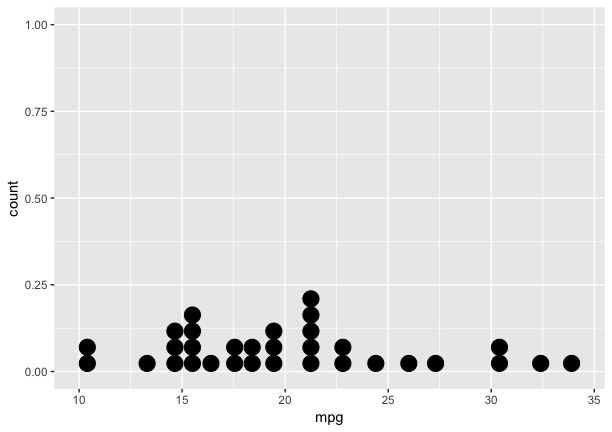
Dot plot histogram

Dot plot figure: y axis is the relative frequency, x axis is the dimension considered, each dot represents one observation, circle: cx=bin center, dot diameter is proportional (factor of 1 in the figure) to bin size.

Popular statistical analysis graphics

Visualizing normality: Q-Q plot and histograms

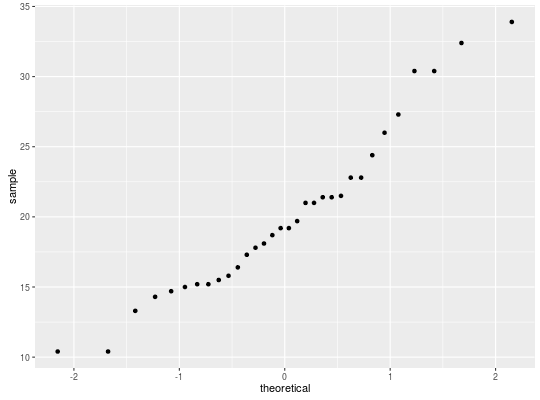
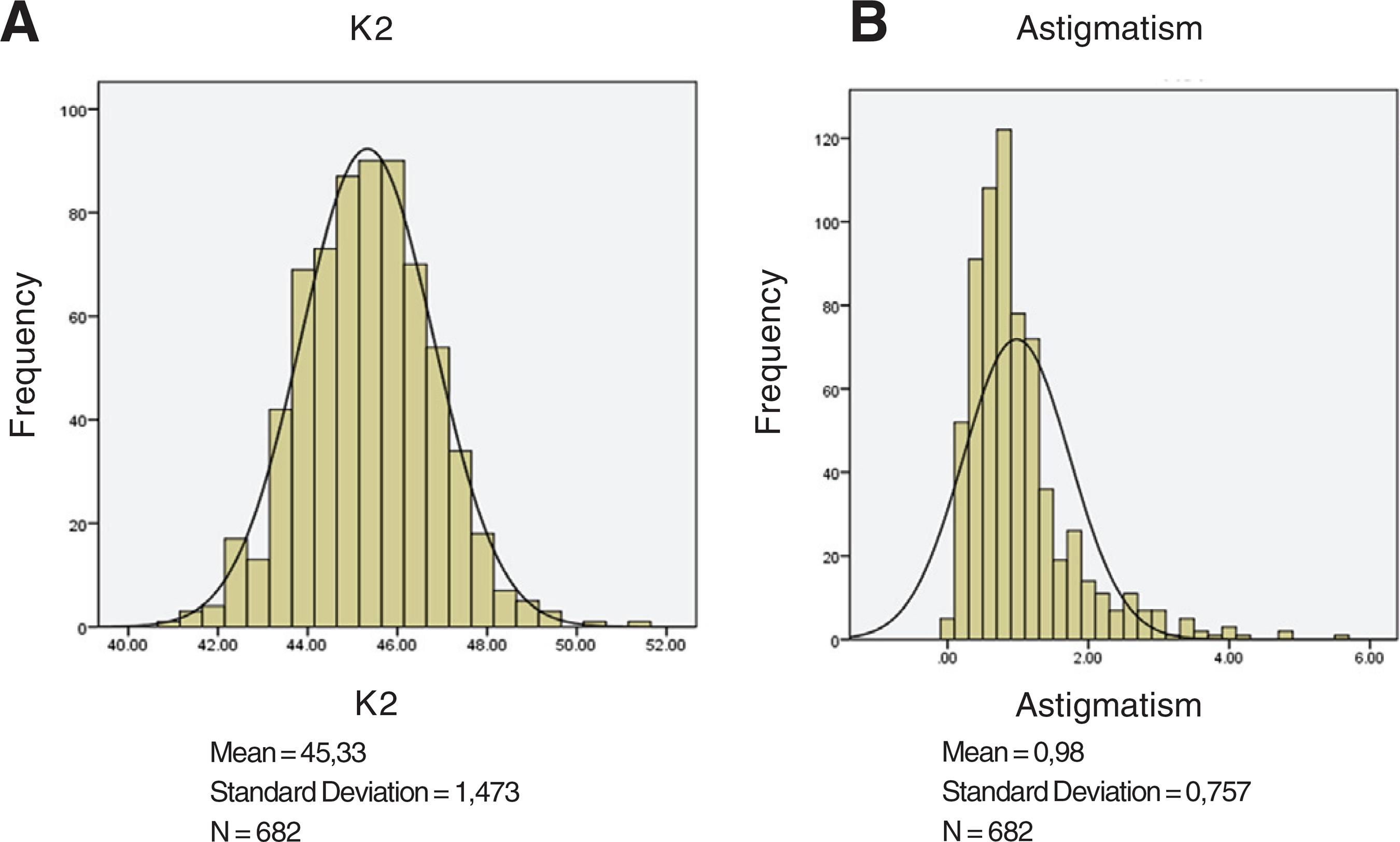
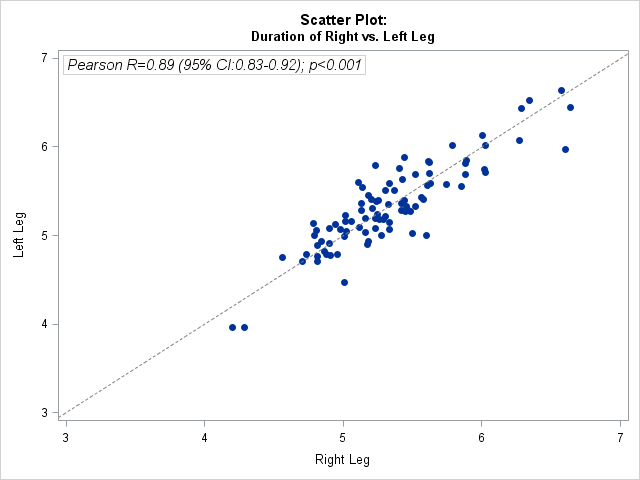
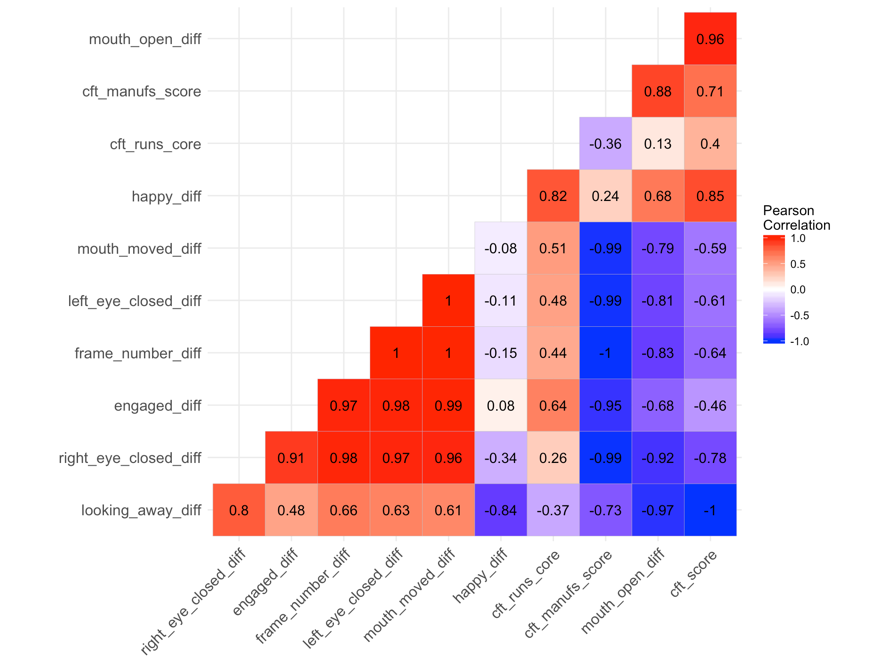
Q–Q (quantile-quantile) plot is a graphical method for comparing two probability distributions by plotting their quantiles against each other. Here we Assess normality by plotting against a normal distribution.

Histogram with superimposed line chart of normal distribution

Visualizing correlations: scatterplots and heatmaps

PCC^* scatterplot and linear regression line.

Heatmap of PCC^* is a graphical tool to assess correlations in multivariate data. Note the diverging R-B color scale.

* Pearson’s correlation coefficients (PCC) or Pearson’s r, is a measure of linear correlation between two sets of data

Visualizing PCA Results

Scree plot

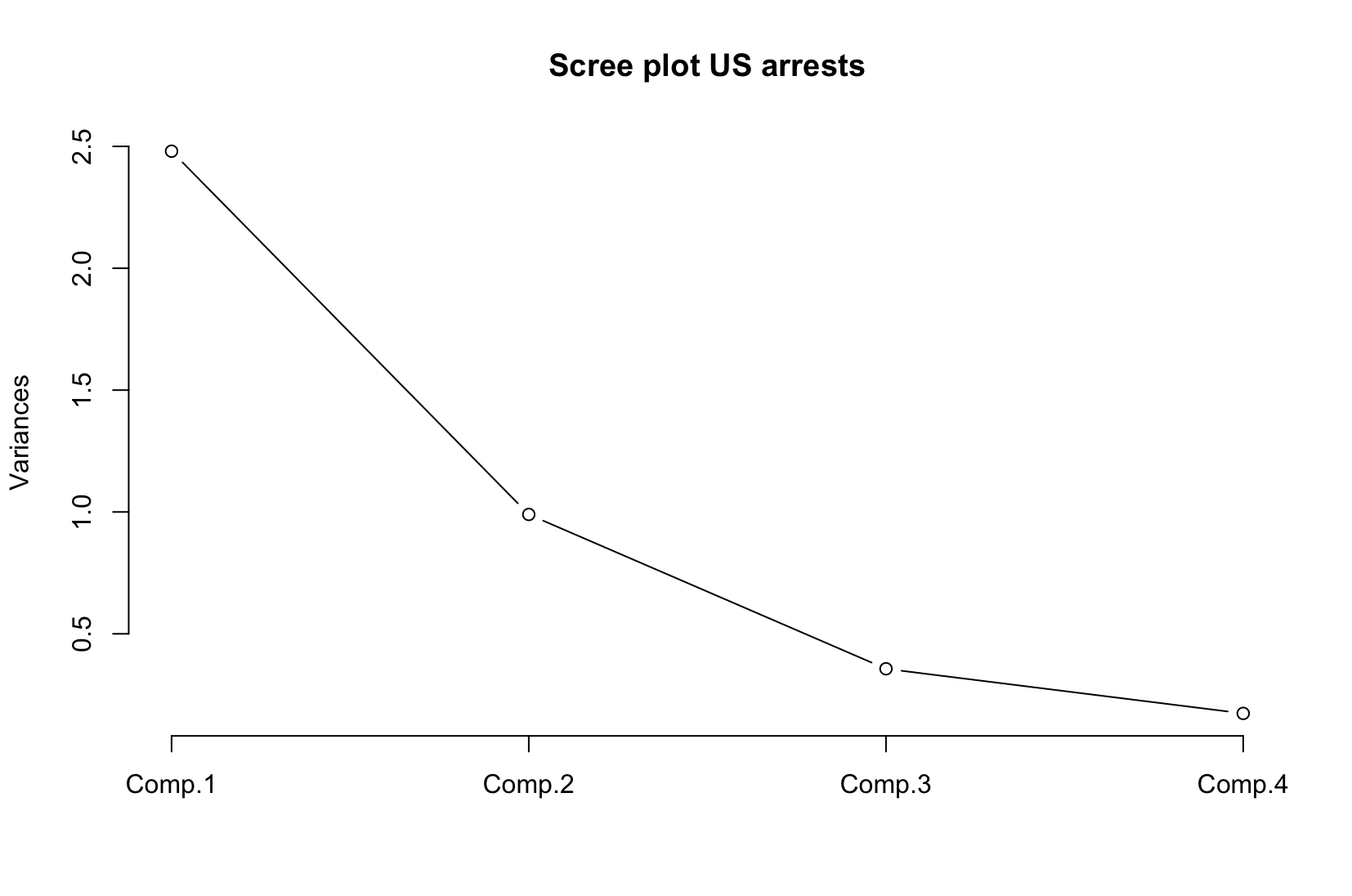
A scree plot shows how PCA^* components explain data variability

Biplot [Gabriel 71]

A Biplot shows samples (points) and variables (vectors) with similar values plotted in the plane of PCA^* components

* Principal Component Analysis (PCA) is commonly used for dimensionality reduction. PCA can be thought of as fitting a p-dimensional ellipsoid to the data, where each axis of the ellipsoid represents a principal component. If some axis of the ellipsoid is small, then the variance along that axis is also small.

Visualizing hierarchical clustering results

Scatterplot of k-means^* results color-coded by cluster with cluster centers and cluster bubbles

Dendrogram (diagram representing a tree) encoding a value

* k-means clustering is a method of vector quantization, originally from signal processing, that aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean (cluster centers or cluster centroid)

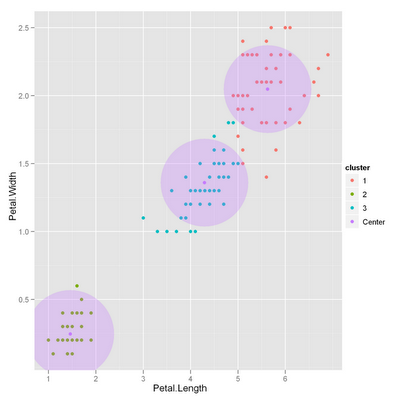
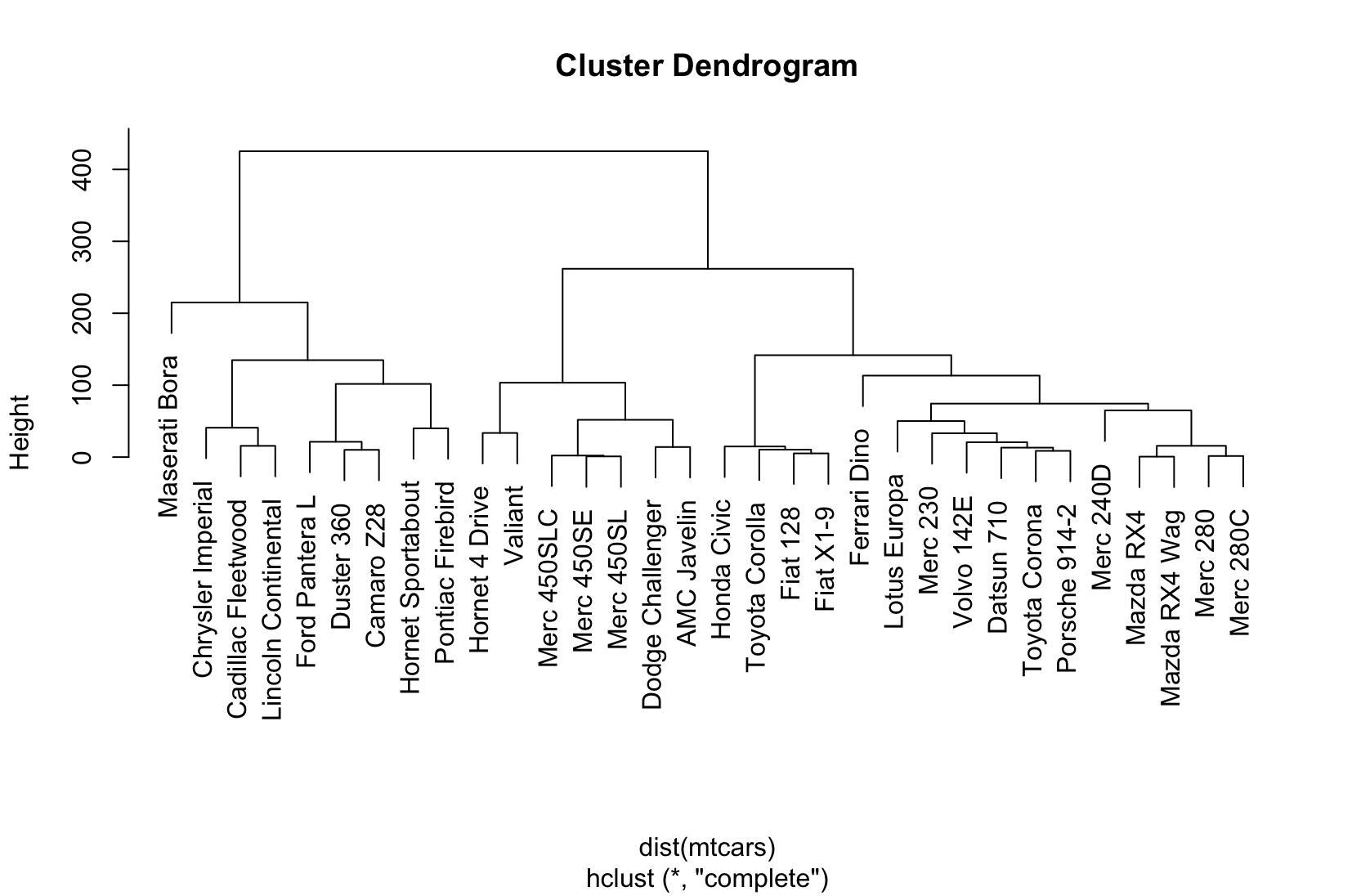
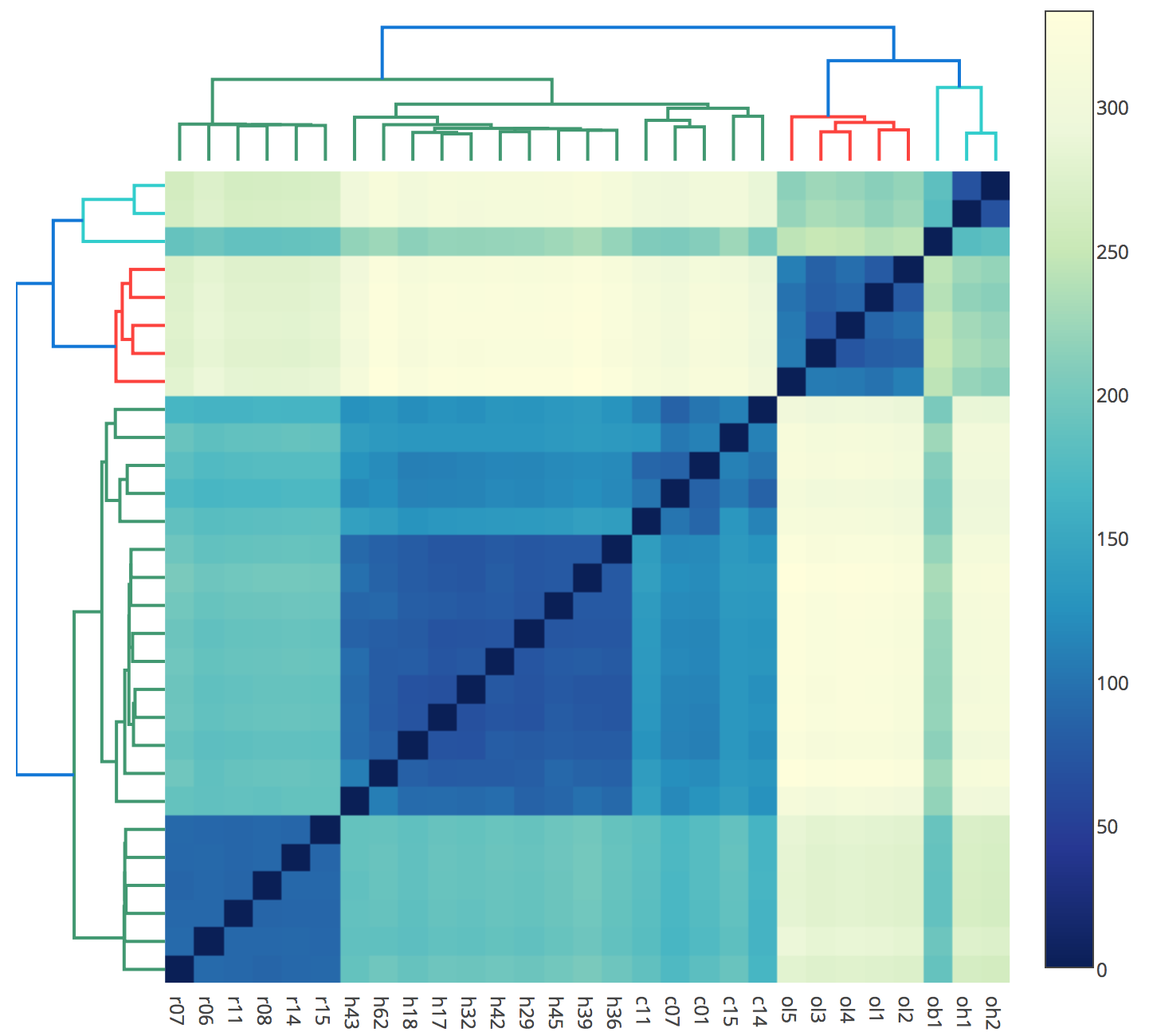
Combination Plot (Combo plot)

Correlations and hierarchical information across variables

Visualizing model performance

Munyamadzi Game Reserve, courtesy of TripAdvisor

Supervised learning

Confusion matrix

Precision and Recall

Specificity and Sensitivity

Visualizing the Confusion matrix: table and heatmap


									# d1:  Int. Derang. (DDWR)  /  Int. Derang. (eDDNR)
									 No Yes
									188 112
	
									Call:
									 randomForest(formula = target, data = df, proximity = TRUE)
													 Type of random forest: classification
														 Number of trees: 500
									No. of variables tried at each split: 11
	
											OOB estimate of  error rate: 3%
									Confusion matrix:
											No  Yes class.error
									No  187   1 0.005319149
									Yes   8 104 0.071428571

Confusion matrix result in R

Khokhlova, et al. "Normal and pathological gait classification LSTM model." Artificial intelligence in medicine 94 (2019)

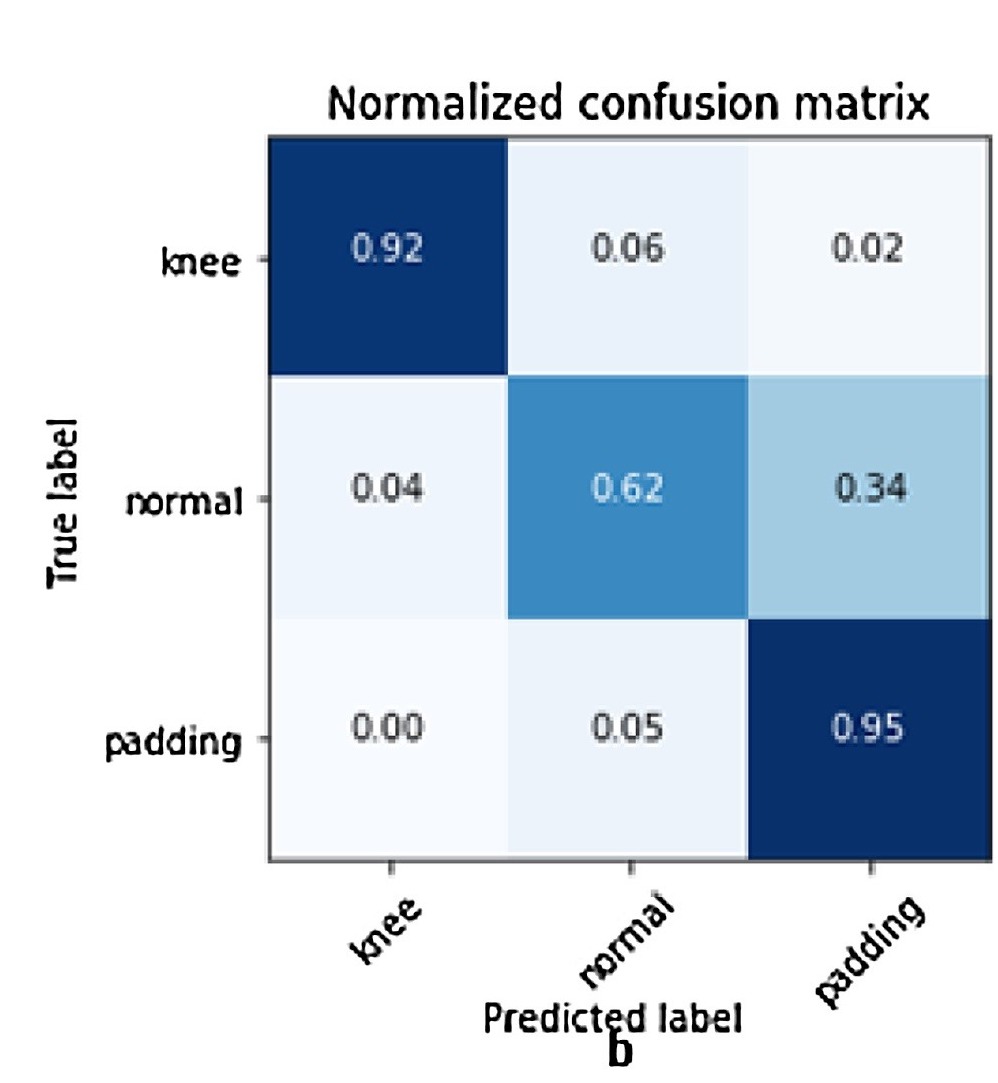
Visualizing the ROC^* curve: line chart

By Sharpr - Own work, CC BY-SA 3.0, Link

ROC^* curve of dental Internal Derangement (DDWR/eDDNR) conditions

* The Receiver Operator Curve (ROC) is a diagnostic tool for binary classifiers with decision threshold

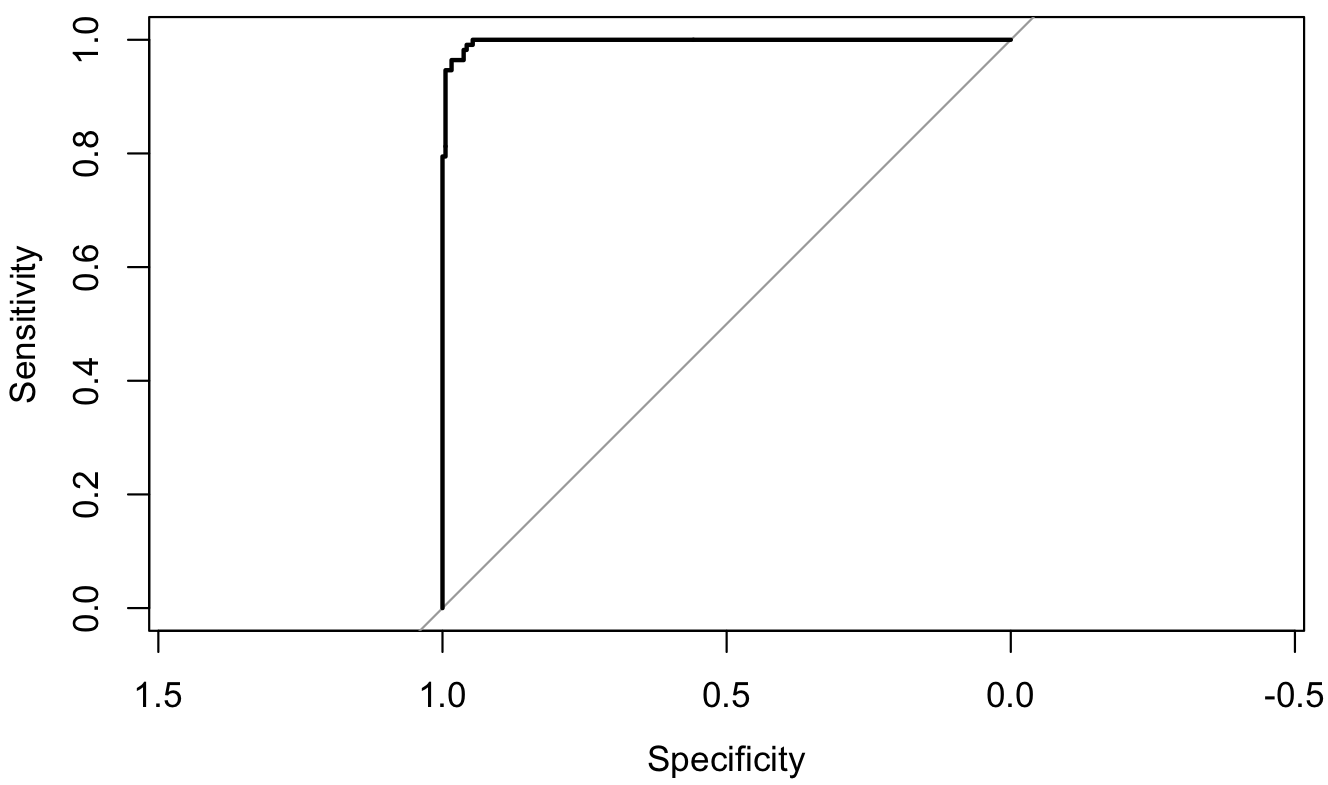
Bars to compare conditions/classifiers

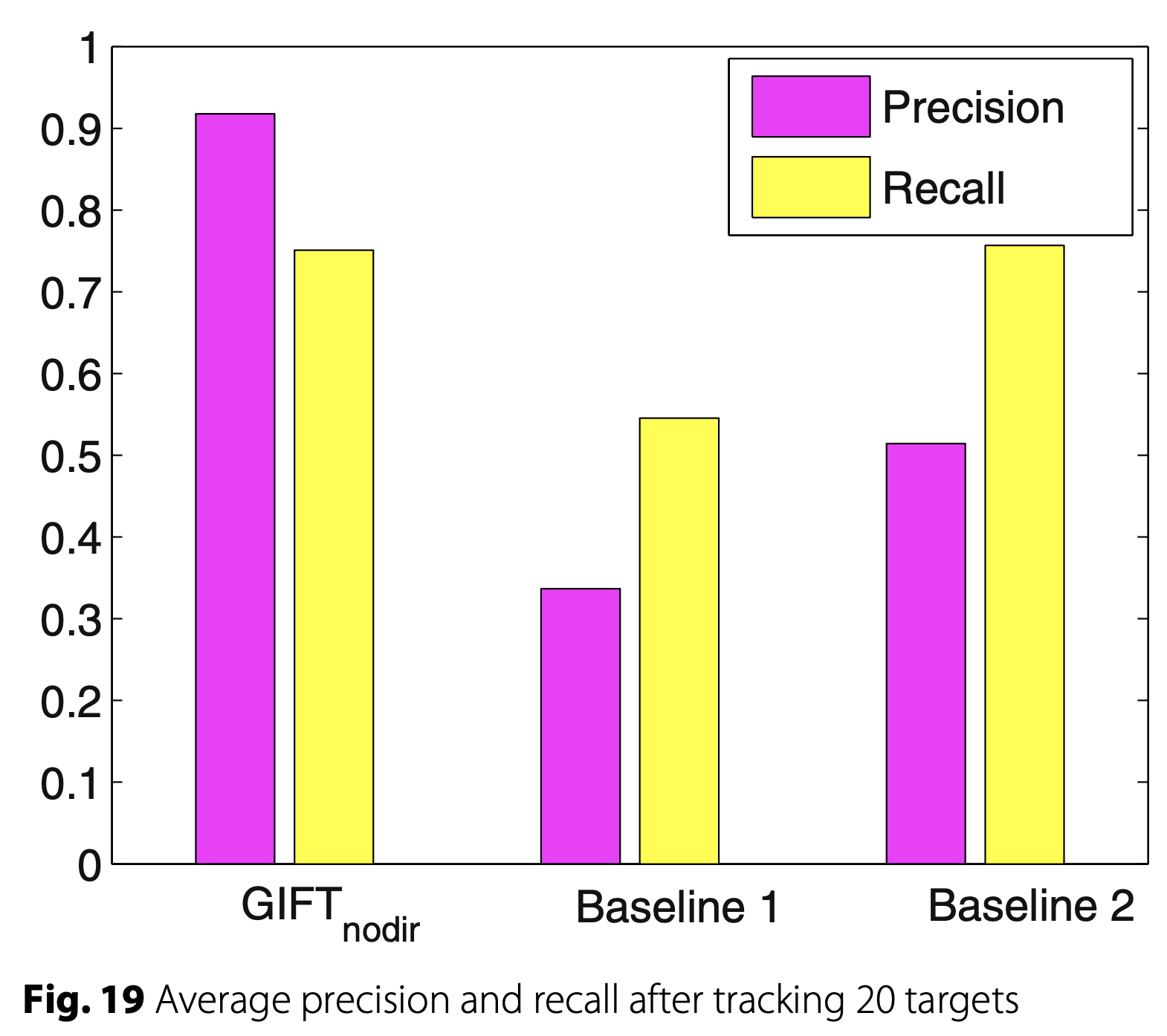
Cai, Y., Lu, Y., Kim, S.H., Nocera, L. and Shahabi, C., 2015, June. Gift: A geospatial image and video filtering tool for computer vision applications with geo-tagged mobile videos. In 2015 IEEE International Conference on Multimedia & Expo Workshops (ICMEW) (pp. 1-6). IEEE.

Tables to compare conditions/classifiers

$$ \text{Precision} = \frac{TP} {TP + FP}$$ $$ \text{Recall} = \frac{TP} {TP + FN}$$

$$ \text{Accuracy} = \frac{TP + TN} {TP + TN + FP + FN}$$ $$ F_1 \text{score} = 2 \cdot \frac{\text{precision} \cdot \text{sensitivity}}{\text{precision} + \text{sensitivity}}$$

Performance of single classifier and multiple classifiers combination. A: Accuracy, P: Precision, R: Recall, F-M: F-measure, AP: Average of Probabilities, MV: Majority Voting, S: SVM, k: k-NN, D: Decision Tree, R: Random Forest.

SVM performance for various features. Accuracy is reported with the format as average accuracy (best accuracy/worst accuracy) across 14 subjects. A: Accuracy, P: Precision, R: Recall and F-M: F-measure. ALL: Gait, Angle, and Graph.

Kao, J.Y., Nguyen, M., Nocera, L., Shahabi, C., Ortega, A., Winstein, C., Sorkhoh, I., Chung, Y.C., Chen, Y.A. and Bacon, H., 2016, October. Validation of automated mobility assessment using a single 3d sensor. In European Conference on Computer Vision (pp. 162-177). Springer, Cham.

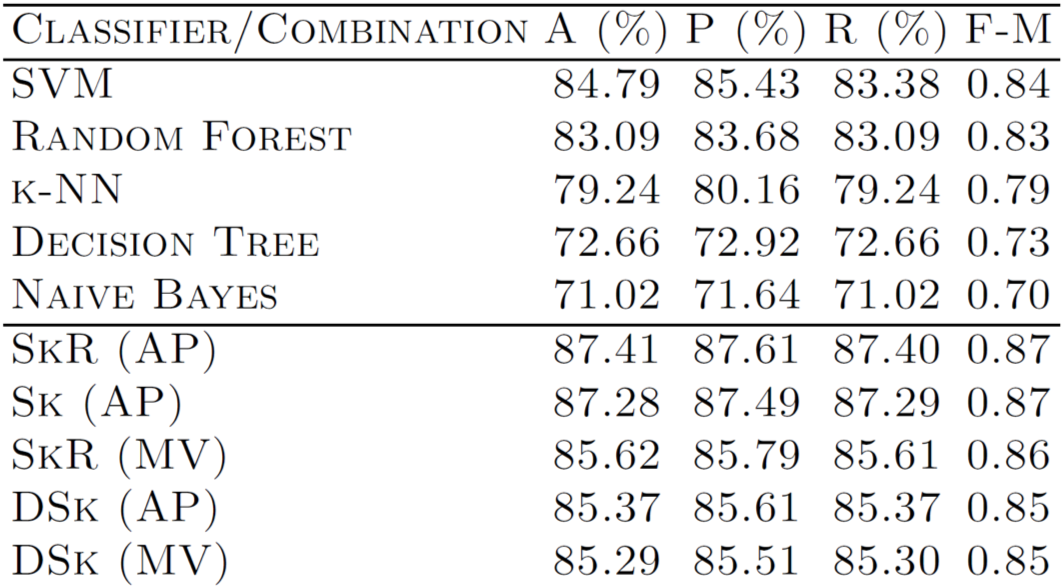
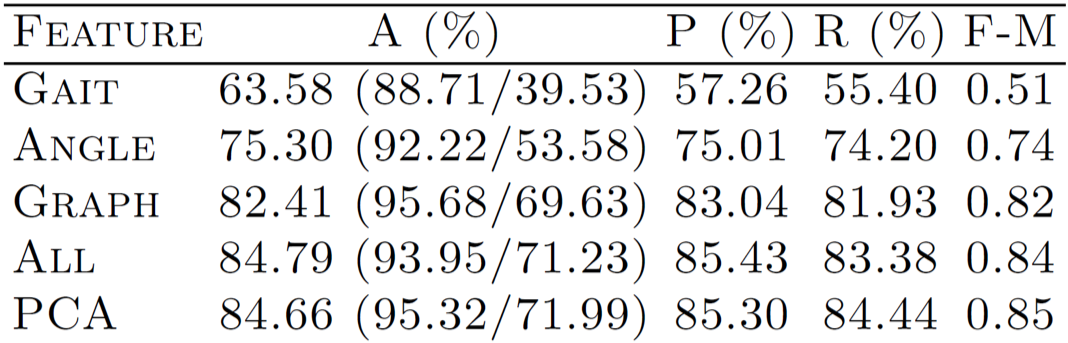
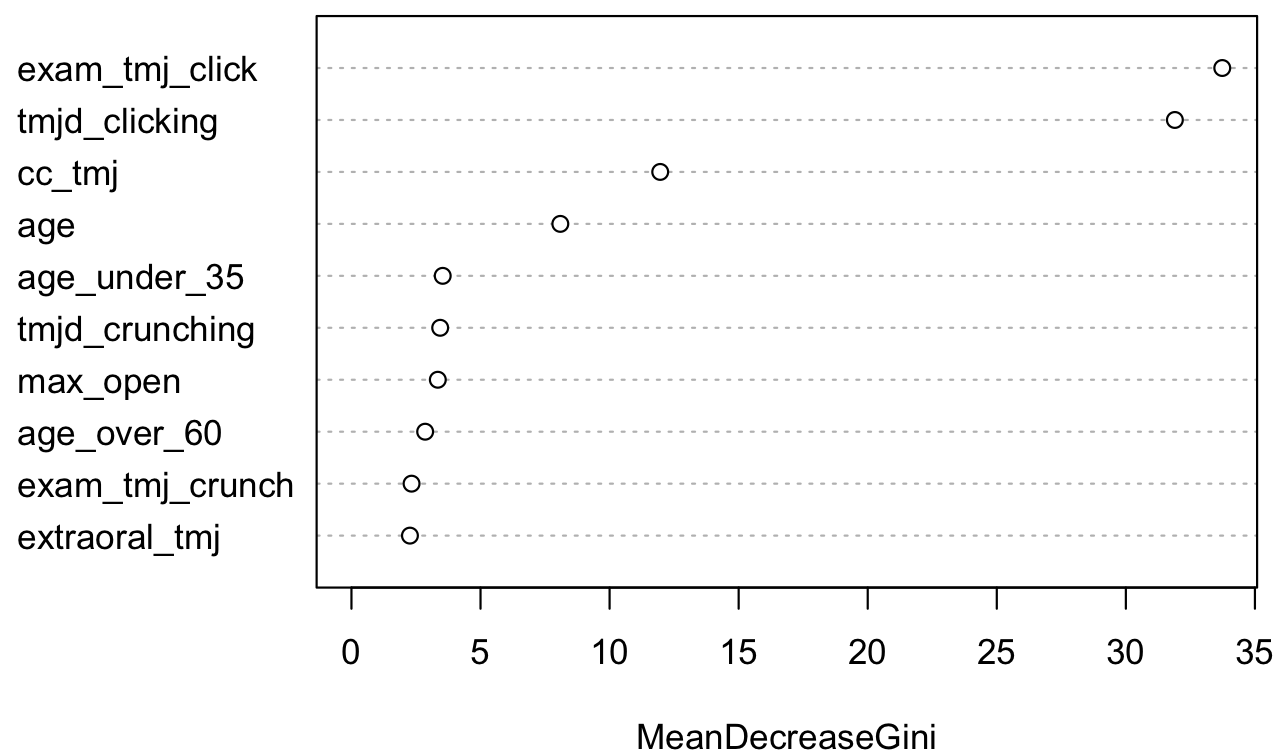
Visualizing feature importance: table and Dot plot


								# d1:  Int. Derang. (DDWR)  /  Int. Derang. (eDDNR)
								 No Yes
								188 112

								Call:
								 randomForest(formula = target, data = df, proximity = TRUE)
											   Type of random forest: classification
													 Number of trees: 500
								No. of variables tried at each split: 11

										OOB estimate of  error rate: 3%
								Confusion matrix:
								    No  Yes class.error
								No  187   1 0.005319149
								Yes   8 104 0.071428571

								Top 10 variables
								   No    Yes
								1  0.990 0.010
								2  0.988 0.012
								3  0.992 0.008
								4  0.108 0.892
								5  0.970 0.030
								6  0.990 0.010
								7  0.962 0.038
								8  0.040 0.960
								9  0.986 0.014
								10 0.042 0.958
								Setting levels: control = No, case = Yes
								Setting direction: controls < cases
								Area under the curve: 0.9974

Classification results showing confidence of top 10 variables

Dot plot of mean decrease Gini

Visualizing Regression models: line chart with Ribbon

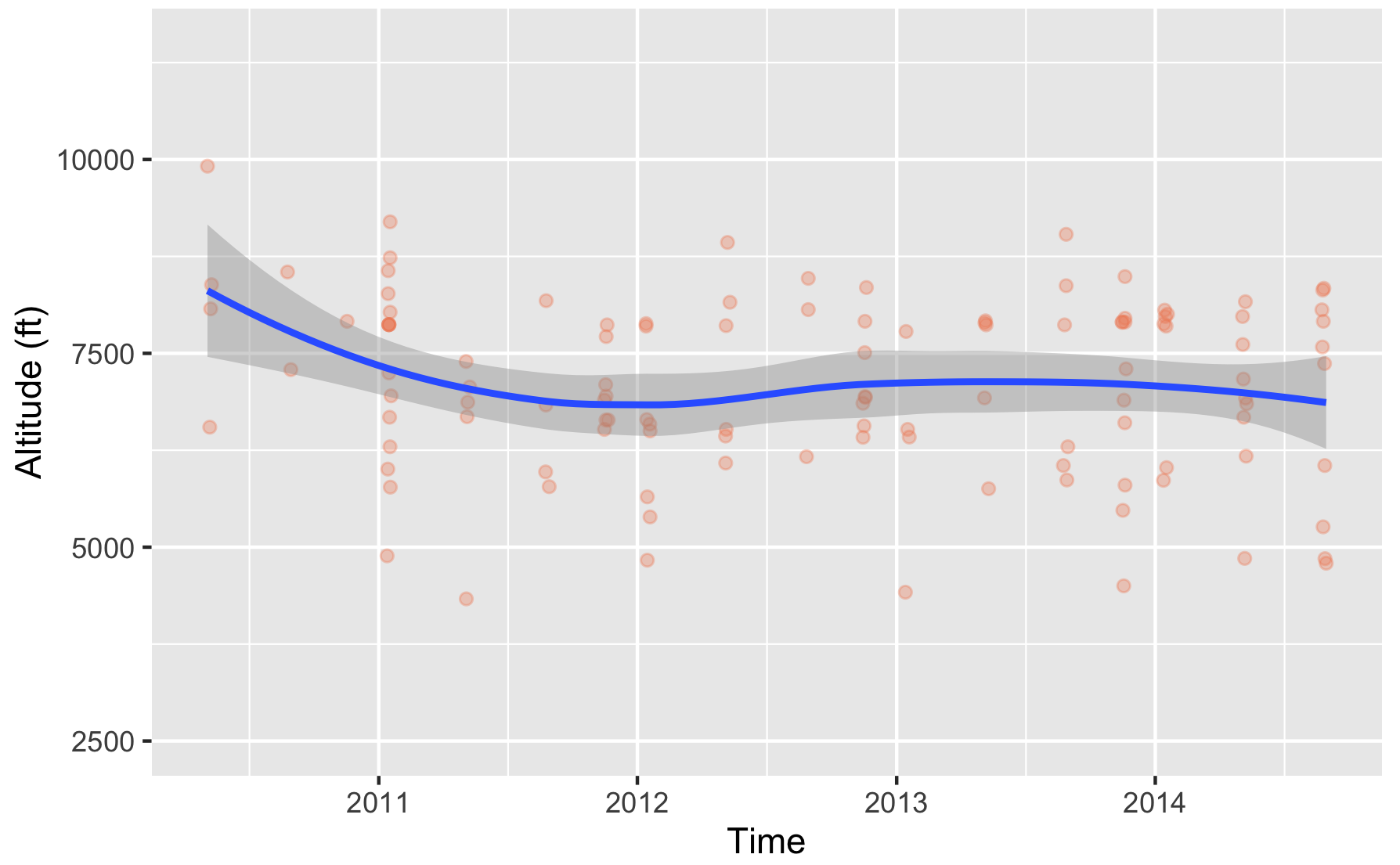
Smooth regression line with 0.95 confidence interval^* *95% confidence interval: interval of values for which a hypothesis test to the level of 5% cannot be rejected $\equiv$ interval has a probability of 95% to contain the true value

Design considerations for statistical graphics

Choose encodings wisely

Color & shape work well with categorical variables

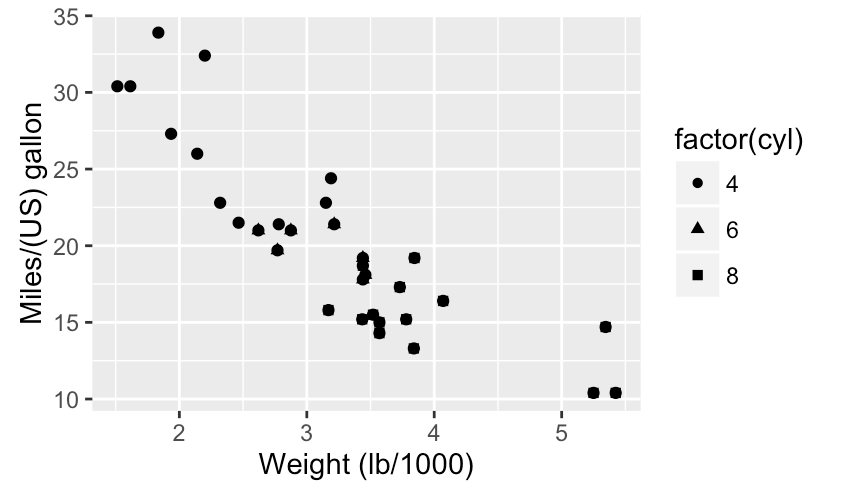
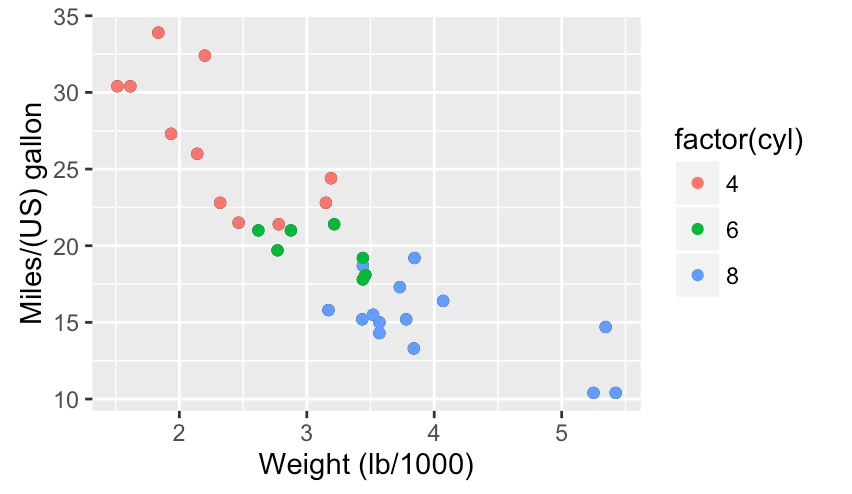
Size works well with continuous variables

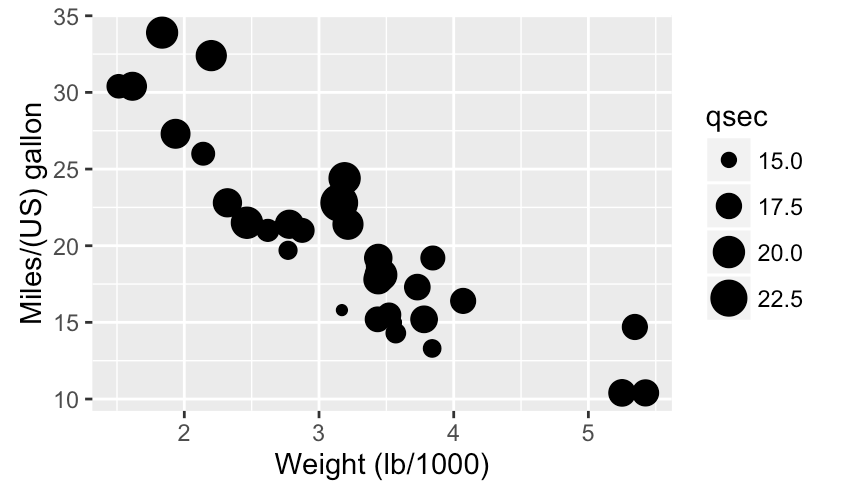
Series work better than complex plots

Faceting/conditioning/latticing/trellising/small multiples

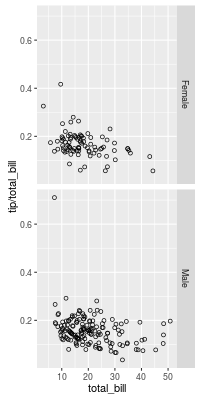
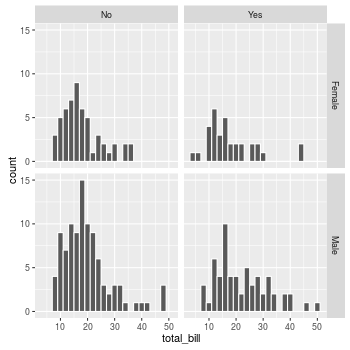
Ways to deal with overplotting

Transparency, outline shape

Add information

Add jitter

Split the data

Summarize the data

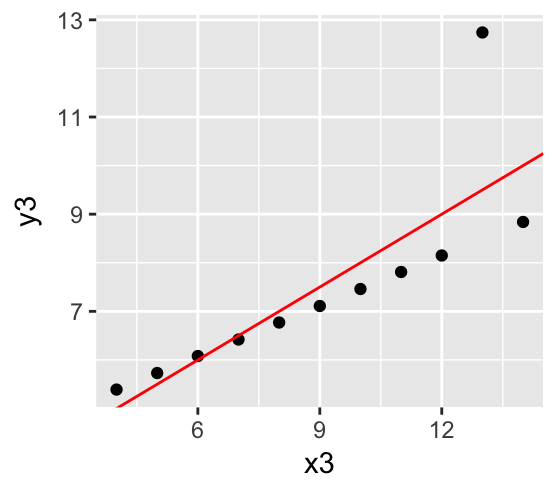
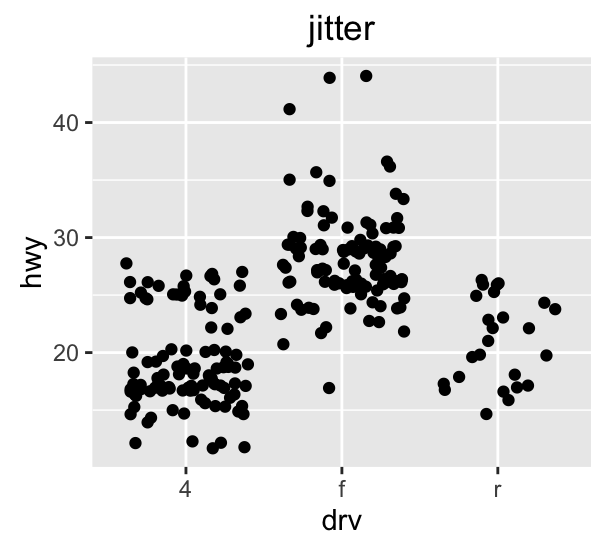
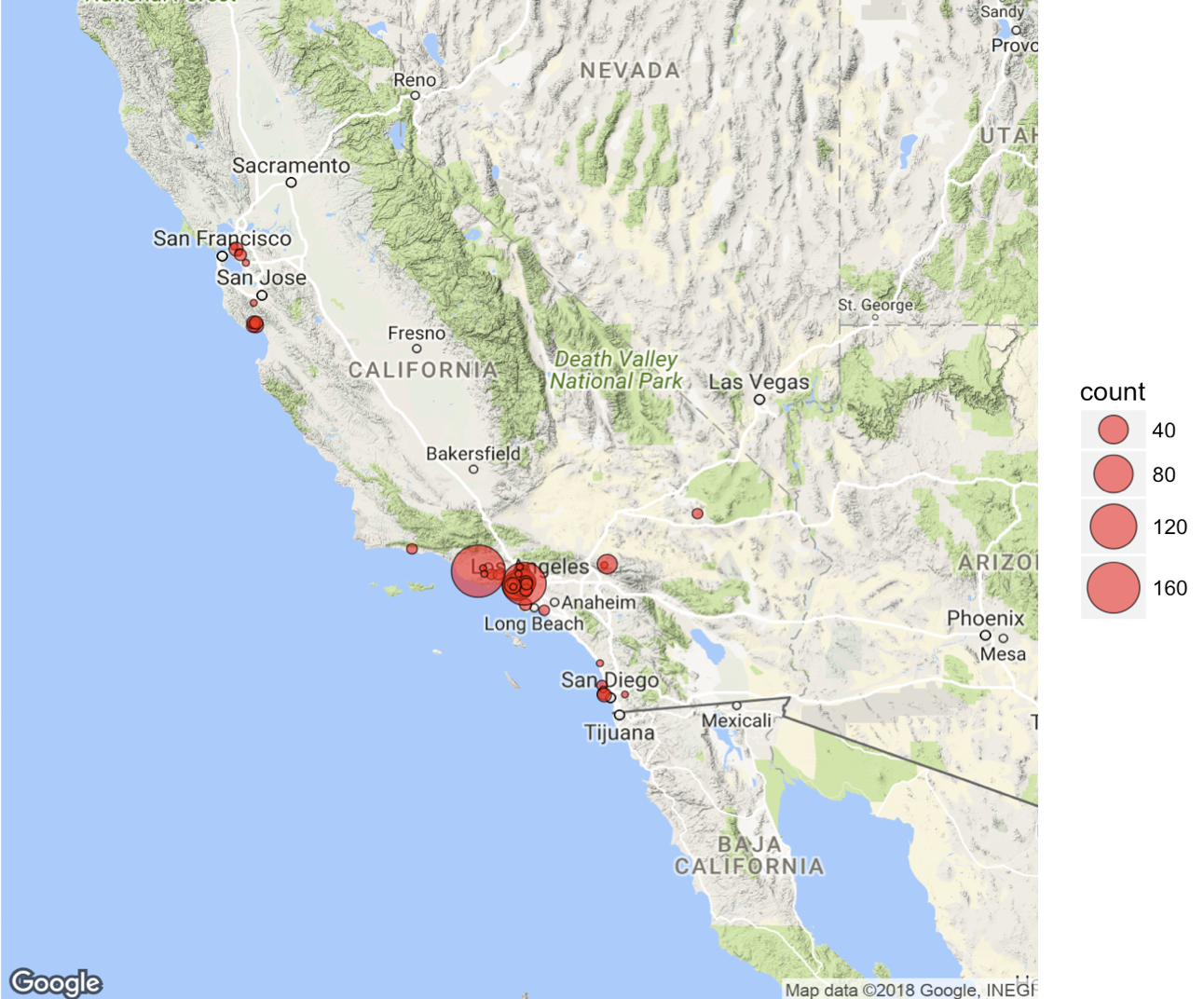
Outline

Basics of statistics and modeling
Statistical graphics
Tools

Visualization tools

Adapted from [Heer 2014]

Dataframe

Table with same length columns
Columns are variables
Rows are observations
Strings can be stored as factors


					> df <- sample_n(mpg, 36)
					> df$manufacturer <- factor(df$manufacturer)
					> df
					# A tibble: 36 x 11
						manufacturer model              displ  year   cyl trans      drv     cty   hwy fl    class
						<fct>        <chr>              <dbl> <int> <int> <chr>      <chr> <int> <int> <chr> <chr>
						1 toyota       camry                2.4  2008     4 auto(l5)   f        21    31 r     midsize
						2 toyota       camry solara         2.4  2008     4 manual(m5) f        21    31 r     compact
						3 dodge        dakota pickup 4wd    4.7  2008     8 auto(l5)   4         9    12 e     pickup
						4 chevrolet    corvette             5.7  1999     8 auto(l4)   r        15    23 p     2seater
						5 audi         a4                   1.8  1999     4 manual(m5) f        21    29 p     compact
						6 jeep         grand cherokee 4wd   4.7  1999     8 auto(l4)   4        14    17 r     suv
						7 hyundai      tiburon              2    1999     4 manual(m5) f        19    29 r     subcompact
						8 dodge        dakota pickup 4wd    3.9  1999     6 manual(m5) 4        14    17 r     pickup
						9 toyota       camry solara         3    1999     6 auto(l4)   f        18    26 r     compact
					10 ford         expedition 2wd       4.6  1999     8 auto(l4)   r        11    17 r     suv
					# ... with 26 more rows
					> summary(df$manufacturer)
					audi  chevrolet      dodge       ford      honda    hyundai       jeep land rover
						3          2          5          5          2          2          2          1
					nissan    pontiac     subaru     toyota volkswagen
						2          1          1          7          3

	Granite	Limestone	Sandstone
Trad	36	0	52
Sport	76	8	41
Bouldering	102	0	13

Not in dataframe format. Can you see why?

rock	type	count
Granite	Trad	36
Granite	Sport	76
Granite	Bouldering	102
Limestone	Trad	0
Limestone	Sport	8
Limestone	Bouldering	0
Sandstone	Trad	52
Sandstone	Sport	41
Sandstone	Bouldering	13

In dataframe format. Can you see why?

Matplotlib

http://matplotlib.org and gallery
Chart typology
Originally emulating the MATLAB® graphics commands
Imperative (functional) programming


						import matplotlib.pyplot as plt
						import numpy as np

						T = np.arange(0.0, 2.0, 0.01)
						S = 1 + np.sin(2*np.pi*t)

						plt.plot(T, S)
						plt.xlabel('time (s)')
						plt.ylabel('voltage (mV)')
						plt.title('About as simple as it gets, folks')
						plt.grid(True)

						plt.show()

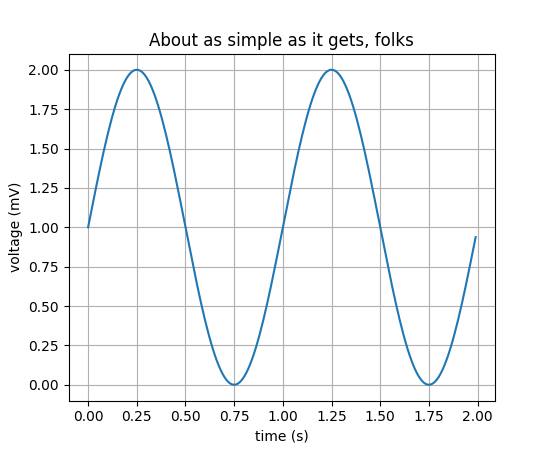
Seaborn

https://seaborn.pydata.org and gallery
Chart typology
High-level interface for statistical graphics based on Matplotlib
Imperative (functional) programming
Support for Pandas dataframes


							import numpy as np
							import seaborn as sns

							x = 5 + np.arange(20) +
							    np.random.randn(20)
							y = 10 + np.arange(20) +
								5 * np.random.randn(20)

							sns.regplot(x, y)


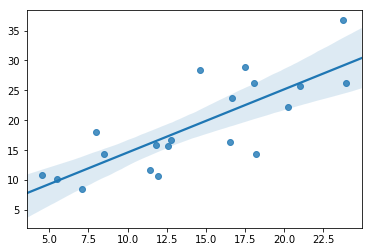
					  Acceleration Cylinders  Displacement Horsepower Miles_per_Gallon Name                      Origin Weight_in_lbs Year
					0 12.0         8          307.0        130.0      18.0             chevrolet chevelle malibu USA    3504          1970-01-01
					1 11.5         8          350.0        165.0      15.0             buick skylark 320         USA    3693          1970-01-01
					2 11.0         8          318.0        150.0      18.0             plymouth satellite        USA    3436          1970-01-01
					3 12.0         8          304.0        150.0      16.0             amc rebel sst             USA    3433          1970-01-01
					4 10.5         8          302.0        140.0      17.0             ford torino               USA    3449          1970-01-01
						...


							import seaborn as sns
							from vega_datasets import data

							cars = data.cars()
							sns.scatterplot(
								x='Horsepower',
								y='Miles_per_Gallon',
								hue='Origin',
								data=cars);

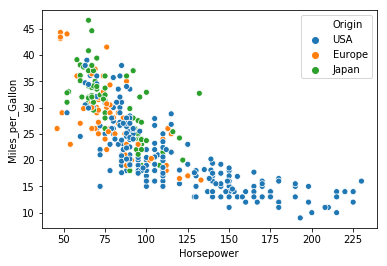
ggplot2

ggplot2 R package and ggg gallery
Visual Analysis Grammar
Support for R dataframes


							mpg cyl disp  hp drat    wt  qsec vs am gear carb
							Mazda RX4      21.0 6 160.0 110 3.90 2.620 16.46  0  1    4    4
							Mazda RX4 Wag  21.0 6 160.0 110 3.90 2.875 17.02  0  1    4    4
							Datsun 710     22.8 4 108.0  93 3.85 2.320 18.61  1  1    4    1
							...


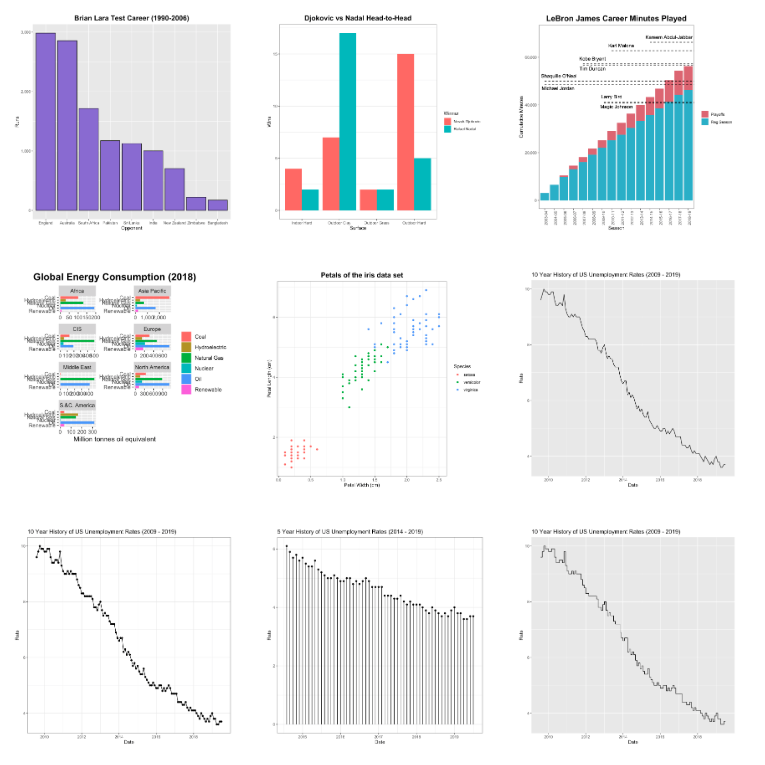
							#ggplot(Data, Mapping) + Geom
							ggplot(mtcars, aes(x=wt, y=mpg)) + geom_point()

plotnine

Plotnine website and gallery
Visual Analysis Grammar
Based on ggplot2 for Python
Support for Pandas dataframes


							               mpg cyl disp  hp drat    wt  qsec vs am gear carb
							Mazda RX4      21.0 6 160.0 110 3.90 2.620 16.46  0  1    4    4
							Mazda RX4 Wag  21.0 6 160.0 110 3.90 2.875 17.02  0  1    4    4
							Datsun 710     22.8 4 108.0  93 3.85 2.320 18.61  1  1    4    1
							...


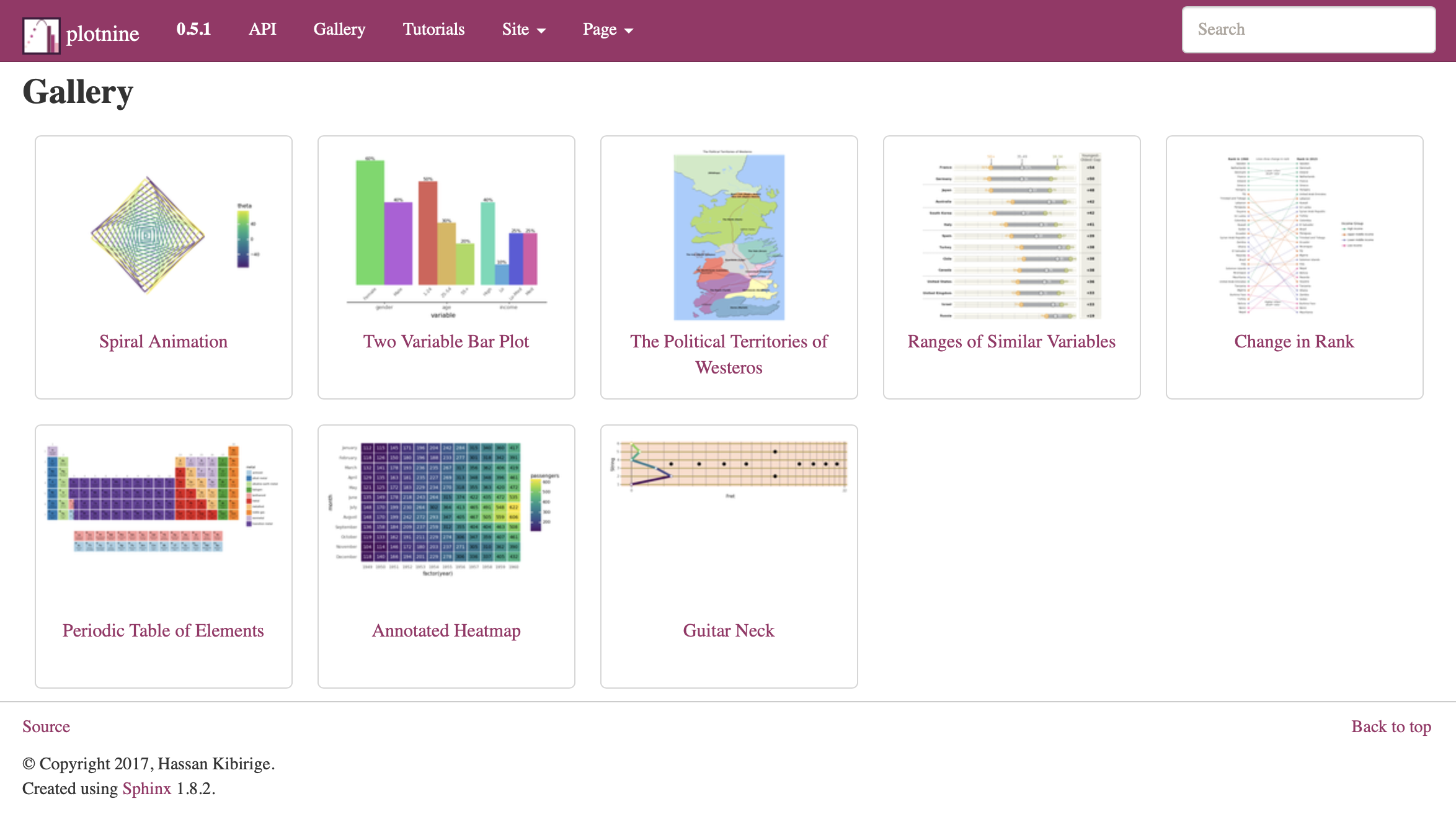
							(ggplot(mtcars, aes('wt', 'mpg', color='factor(gear)'))
							+ geom_point()
							+ stat_smooth(method='lm')
							+ facet_wrap('~gear'))

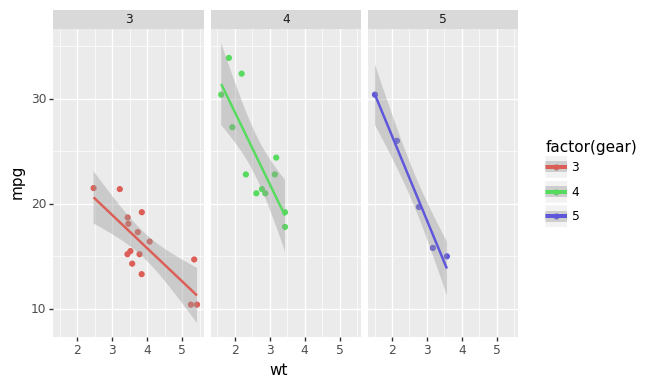
Altair

Altair website and gallery
Visual Analysis Grammar
Declarative synthax
Statistical visualization library
Based on Vega and Vega-Lite
Support for Pandas dataframes


								import altair as alt

								# load a simple dataset as a pandas DataFrame
								from vega_datasets import data
								cars = data.cars()

								alt.Chart(cars).mark_point().encode(
								  x='Horsepower',
								  y='Miles_per_Gallon',
								  color='Origin',
								).interactive()

Components of the Grammar of graphics^*

Graphic defined by a grammar of components

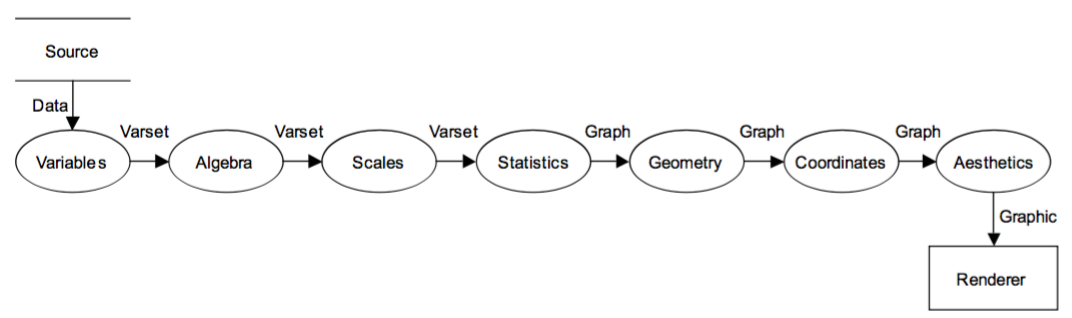
DATA: a set of data operations that create variables from datasets,
TRANS: variable transformations, e.g., rank,
SCALE: scale transformations, e.g., log,
COORD: a coordinate system, e.g., polar,
ELEMENT: graphs, e.g., points, and their aesthetic attributes, e.g., color,
GUIDE: one or more guides, e,g., axes, legends.

*Wilkinson, L. (2005), The Grammar of Graphics (2nd ed.). Statistics and Computing, New York: Springer

Layered Grammar of Graphics^* [Wickham 2010]

Defaults Data Mapping^**	A default dataset and set of mappings from variables to aesthetics
Layer Data Mapping Geom Stat Position	One or more layers, each composed of a geometric object, a statistical transformation, a position adjustment, and optionally, a dataset and aesthetic mappings
- Coord - Facet	A coordinate system The facetting specification

A theme controls the finer points of display, like the font size and background color * implemented in ggplot2 ** Mapping of visual properties to data columns is referred to as an aesthetic mapping

Minimal ggplot2 plot

3 components required in every ggplot2 plot: data, aesthetic mapping, Geom

Defaults

Data
Mapping

Layer

Data
Mapping
Geom
Stat
Position

Scale

Coord
Facet


							ggplot(data=mpg, aes(x=hwy, y=cty)) + geom_point() #Defaults
							ggplot(mpg, aes(hwy, cty)) + geom_point() #positional args
							ggplot(mpg) + geom_point(aes(hwy, cty))  #Mapping in layer

							# Same using a variable
							p <- ggplot(mpg, aes(hwy, cty))  #set Defaults
							p + geom_point()  #add Layer with Geom

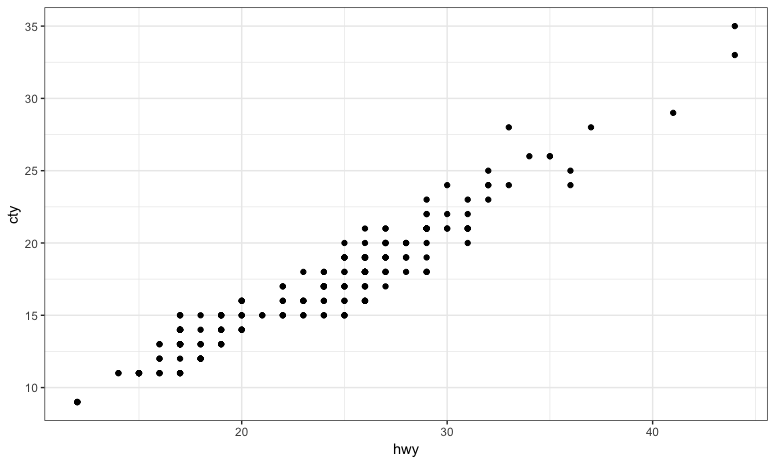
aes() references variables in the dataframe


					# mtcars dataset:
					                    mpg  cyl  disp  hp drat    wt  qsec vs am gear carb
					Mazda RX4           21.0   6 160.0 110 3.90 2.620 16.46  0  1    4    4
					Mazda RX4 Wag       21.0   6 160.0 110 3.90 2.875 17.02  0  1    4    4
					Datsun 710          22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1

					aes(x = mpg, y = wt)
					#> Aesthetic mapping: 
					#> * `x` -> `mpg`
					#> * `y` -> `wt`
					
					# You can also map aesthetics to functions of variables
					aes(x = mpg ^ 2, y = wt / cyl)
					#> Aesthetic mapping: 
					#> * `x` -> `mpg^2`
					#> * `y` -> `wt/cyl`
					
					# Or to constants
					aes(x = 1, colour = "smooth")
					#> Aesthetic mapping: 
					#> * `x`      -> 1
					#> * `colour` -> "smooth"

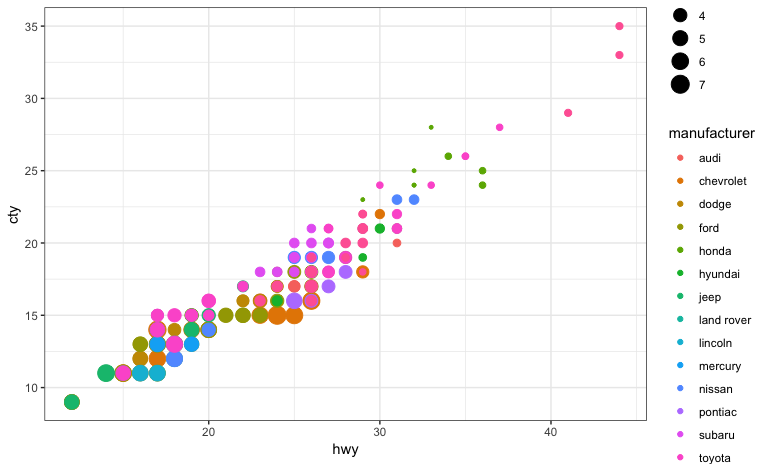
Aesthetics Mappings


					ggplot(mpg, aes(x=hwy, y=cty, color=manufacturer, size=displ)) + geom_point()  #x, y
					ggplot(mpg, aes(hwy, cty, color=manufacturer, size=displ)) + geom_point()  #color
					ggplot(mpg, aes(hwy, cty), color=manufacturer, size=displ) + geom_point()  #bad

					ggplot(mpg, aes(hwy, cty, col=manufacturer, size=displ)) + geom_point()  #col
					ggplot(mpg, aes(hwy, cty, colour=manufacturer, size=displ)) + geom_point()  #colour

					ggplot(mpg, aes(hwy, cty)) + geom_point(aes(color=manufacturer, size=displ))
					ggplot(mpg, aes(hwy, cty)) + geom_point(color=manufacturer, size=displ)  #bad!

Adding layers

Defaults

Data
Mapping

Layer

Data
Mapping
Geom
Stat
Position

Scale

Coord
Facet


							> ggplot(mpg, aes(hwy, cty)) +  #Defaults
							  geom_point() +  #add Geom point Layer
							  geom_smooth()  #add Geom smooth Layer (regression)

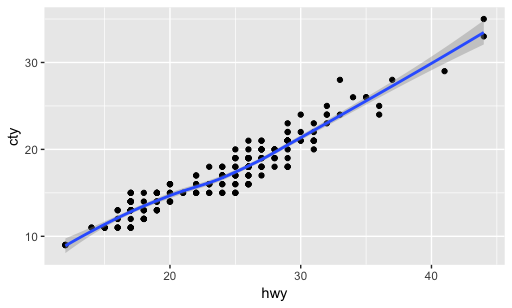
Basic named plots

All understand x, y, color and size aesthetics.
Filled geoms also understand fill.

Scatterplot	geom_point()
Text	geom_text()
Bar chart	geom_bar()
Line chart	geom_line()
Area chart	geom_area()
Dot plot	geom_dotplot()
Histogram	geom_histogram()
Frequency polygon	geom_freqpoly()
Box plot	geom_boxplot()
Violin plot	geom_violin()

$$y \sim x$$

model formula: tilde Operator separates the left- and right-hand sides


					# Multiple linear regression
					fit <- lm(y ~ x1 + x2 + x3, data=mydata)
					summary(fit) # show results

Faceting


					t <- ggplot(mpg, aes(cty, hwy)) + geom_point()

	New notation	Old formula interface^*
	`t + facet_grid(cols = vars(lf))`	`t + facet_grid(. ~ lf)`
	`t + facet_grid(rows = vars(year))`	`t + facet_grid(year ~ .)`
	`t + facet_grid(year, lf)`	`t + facet_grid(years ~ lf)`
	`t + facet_wrap(facets=vars(lf))`	`t + facet_grid(~ lf)`

^*the dot in the formula (i.e., . ~ x or y ~ .) indicates no faceting on this dimension.

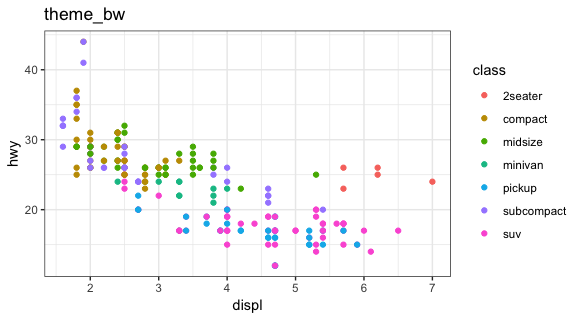
Default themes and extra themes


				p <- ggplot(mpg, aes(displ, hwy, color=class)) + geom_point()
				p + theme_bw() + ggtitle("theme_bw")
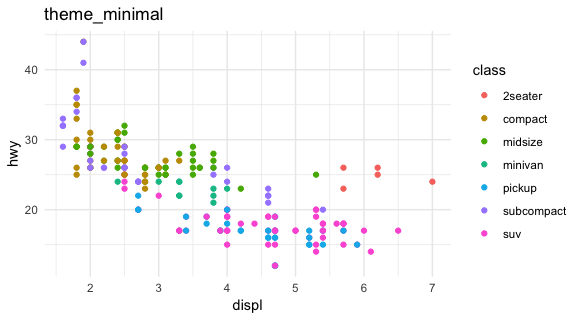
				p + theme_minimal() + ggtitle("theme_minimal")

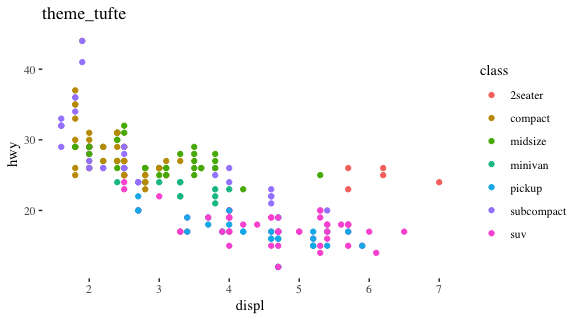
				library(ggthemes)  #extra themes
				p + theme_tufte() + ggtitle("theme_tufte")

				theme_set(theme_bw())  #sets the theme for all subsequent ggplot plots

Extra themes in package ggthemes

GGPLOT 2 layered grammar


					ggplot(iris, aes(x=Sepal.Length, y=Sepal.Width, color=Species, size=Petal.Length)) + geom_point()

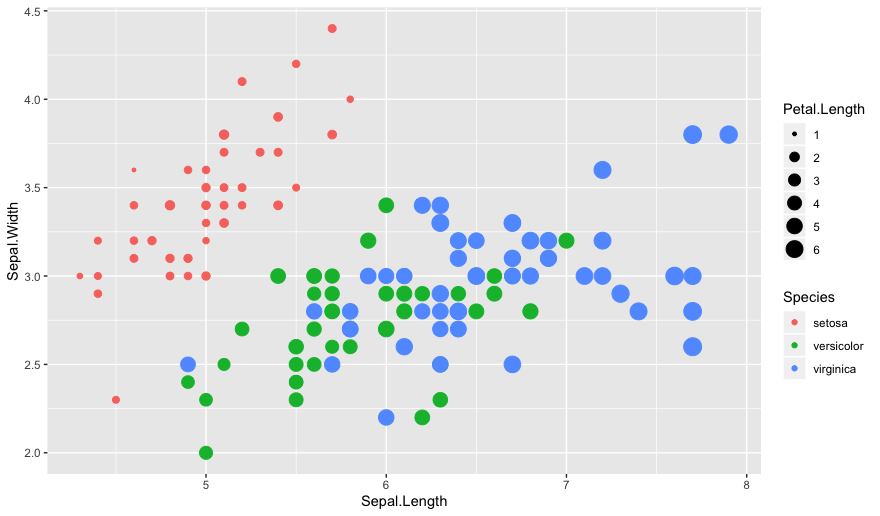
Use geom_point(shape=1) to draw circle outline

Tableau visual grammar

With data read from CSV:
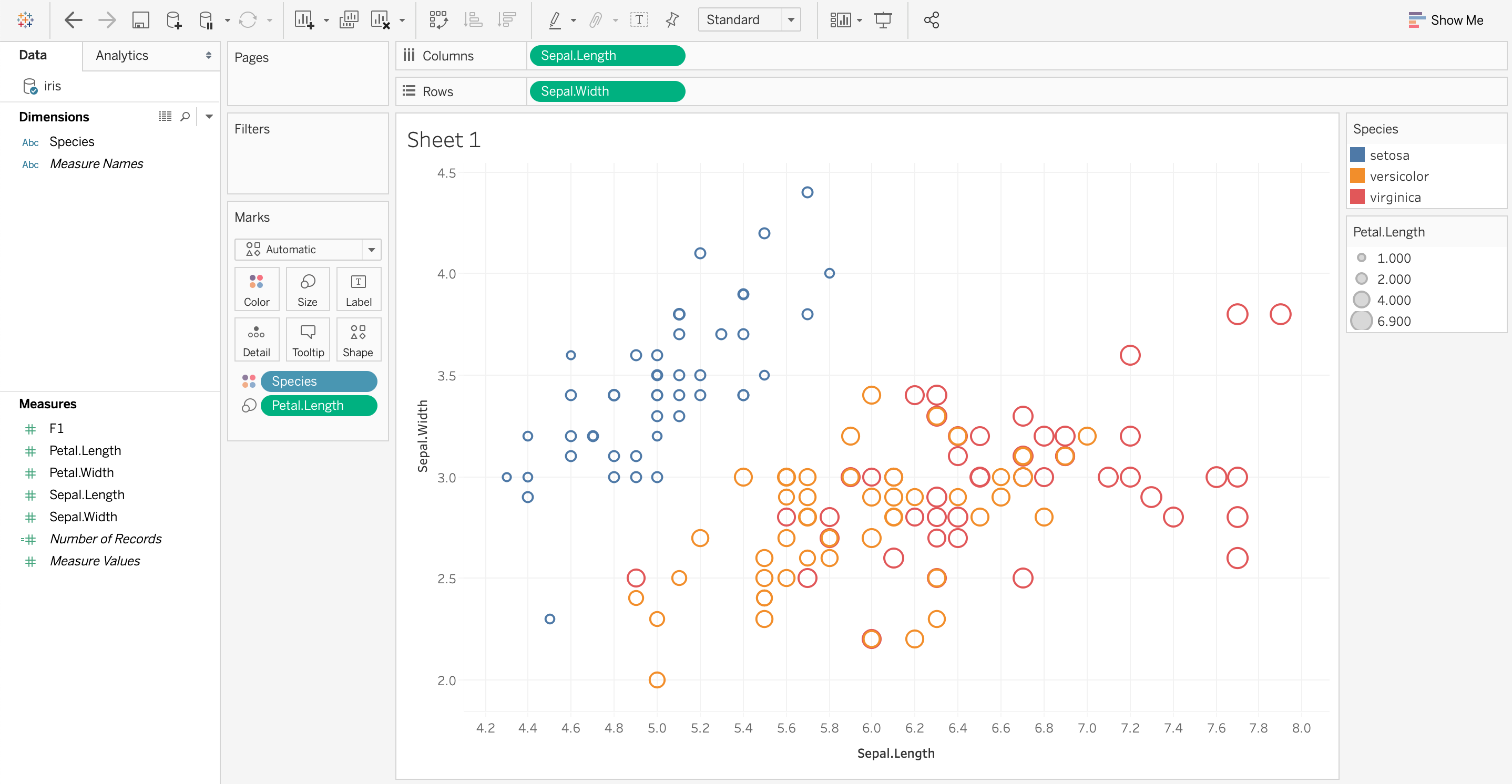
Dimensions ↔ categorical visual variables
Measures ↔ numerical visual variables

Tableau vs. GGPLOT2

Mappings:
x ↔ Column
y ↔ Rows

DSCI 554 lecture 9

Statistics review, statistical graphics

Outline

Statistics

Types of statistics

Nomenclature

What are the independent and dependent variables?

Measures of order

Quantiles

Measures of central tendency

Skewness

Frequency & Relative frequency

Outline

Importance of graphing before analysis [Anscombe73]

Scatterplot

Shows distribution modes, skewness, outliers

Scatterplot matrix

Shows distribution for multivariate data

Stripchart (1D scatterplot)

Good for comparison across categories

Boxplot or box-and-whisker plot [Tuckey 1969]

Quartiles, distribution skewness, tails, outliers (not modes: unimodal distribution)

Boxplot anatomy

Frequency distribution table

Often shown with ordered data, relative frequency and cumulative frequency

Bar charts of frequencies

Stem-and-leaf plot

Shows the data and data distribution (skewness, modes, tails, outliers)

Steps to build a stem-and-leaf plot

Histogram [Pearson 1895]

Shows skewness, modes, tails, outliers

Steps to build an histogram

Frequency polygon

Shows skewness, modes, tails, outliers

Dot plot histogram

Popular statistical analysis graphics

Visualizing normality: Q-Q plot and histograms

Visualizing correlations: scatterplots and heatmaps

Visualizing PCA Results

Visualizing hierarchical clustering results

Combination Plot (Combo plot)

Visualizing model performance

Supervised learning

Confusion matrix

Precision and Recall

Specificity and Sensitivity

Visualizing the Confusion matrix: table and heatmap

Visualizing the ROC* curve: line chart

Bars to compare conditions/classifiers

Tables to compare conditions/classifiers

Visualizing feature importance: table and Dot plot

Visualizing Regression models: line chart with Ribbon

Design considerations for statistical graphics

Choose encodings wisely

Series work better than complex plots

Ways to deal with overplotting

Outline

Visualization tools

Dataframe

Matplotlib

Seaborn

ggplot2

plotnine

Altair

Components of the Grammar of graphics*

Layered Grammar of Graphics* [Wickham 2010]

Minimal ggplot2 plot

3 components required in every ggplot2 plot: data, aesthetic mapping, Geom

aes() references variables in the dataframe

Aesthetics Mappings

Adding layers

Basic named plots

Faceting

Default themes and extra themes

GGPLOT 2 layered grammar

Tableau visual grammar

Tableau vs. GGPLOT2

Visualizing the ROC^* curve: line chart

Components of the Grammar of graphics^*

Layered Grammar of Graphics^* [Wickham 2010]